2021年 神奈川県公立高校入試 数学 解説
神奈川県の公立高校を志望する皆さん、神奈川県の過去問を使って力試しをしたい皆さんへ。
今回は2021年度の数学の問題について検討してみましょう。
2021年度の入試はCOVID-19の影響で出題範囲から中3該当部分が一部削られています。
そのため他年度との単純な比較はできませんので、ご注意ください。
問題をお持ちでない方は以下のリンクからでも入手できます。
事前に全ての問題に取り組み、自分なりにどこまで考えられたかをまとめてから解説をお読みください。
各小問の出だしには正解率を添えておきます。
問1
(ア)毎年通りの正負の数の加減問題です。(96.4%)
\(-9-(-5)=-9+5=-4\)とテンポよく解きます。
暗算で正解が出せることがベストですが、落ち着くためにあえて途中式を書いても良いです。
符号ミスをしていないか、必ずペン先で確認しましょう。
(イ)正負の数の加減問題です。(92.7%)
例年であれば正負の数の加減問題は2問出ません。
この辺りが注意したいところです。
恐ろしいのは、問題が分数になっただけで3.7%正解率が落ちている点ですね。
いかに小学生段階での算数から基礎が抜け落ちている人がいるのかということです。
名門公立高校合格のためには、ます算数を徹底しましょう。
\begin{eqnarray} -\frac{5}{6}-\frac{3}{4}&=&\frac{-10-9}{12}\\ &=&-\frac{19}{12} \end{eqnarray}通分の際に、符号ごと分子に乗せましょう。
また、分母は通分したものをひとまとめにした表記をお勧めします。
(ウ)単項式の乗法・除法問題です。
見た目で暗算も結構ですが、少しでも不安ならば必ず途中式を書きましょう。
この問題は全体を分数として書き表せば、約分として処理する意識でミスが減らせます。
横並びではなく上下です。
\begin{eqnarray} 8ab^2\times 3a\div 6a^2b&=&\frac{8ab^2\times 3a}{6a^2b}\\ &=&4b \end{eqnarray}2021年問題では扱った単項式が全て正の数です。
符号ミスの心配はありませんが、例年では負の数もここで扱われるので注意します。
(エ)文字式分数の加法減法問題です。(88.7%)
通分ミス・符号の分配法則のミスを防ぎます。
苦手であれば一度必ず途中式に書くこと、分配法則は必ずペン先で数字・文字を指して確認することで対応します。
よくある出題形式ですが、後ろの(カッコ)内の符号が与式では正と負で異なっています。
展開後も符号が異なっていることを確認できれば、ミスを自分で発見できます。
与式で(カッコ)内の符号が同じならば展開しても同じ、異なるなら異なるというリズムです。
\begin{eqnarray} \frac{3x + 2y}{5} – \frac{x – 3y}{3} &=& \frac{3(3x + 2y) – 5(x – 3y)}{15} \\ &=& \frac{9x + 6y – 5x + 15y}{15} \\ &=& \frac{4x + 21y}{15}\\ \end{eqnarray}(オ)平方根の計算問題です。(90.3%)
式の展開と整理ですので、中3の1学期に練習を積んでおけば足ります。
文字式だろうが分数だろうが小数だろうが平方根だろうが、いつでも同じ行動をとりましょう。
何か違うルールで計算をすることなどないと心得てください。
\begin{eqnarray} (2+\sqrt 7)(2-\sqrt 7)+6(\sqrt 7+2)&=&2^2-\sqrt 7^2+6\sqrt 7+12\\ &=&4-7+12+6\sqrt 7\\ &=&9+6\sqrt 7 \end{eqnarray}問1の総評としては、例年同様に満点でクリアするべきレベルです。
大学進学を目指す公立高校合格のために、絶対に満点でクリアしましょう。
問2
(ア)因数分解の基礎問題です。(92.3%)
例年であれば問1に入っているような問題です。
\((x+6)=A\)などと置換して式を簡単にしてしまうのが一般的でしょう。
\begin{eqnarray} (x+6)^2-5(x+6)-24&=&A^2-5A-24\\ &=&(A-8)(A+3)\\ &=&\{(x+6)-8\}\{(x+6)+3\}\\ &=&(x-2)(x+9) \end{eqnarray}もちろん強引に展開しても構いません。
\begin{eqnarray} (x+6)^2-5(x+6)-24&=x^2+12x+36-5x-30-24\\ &=&x^2+7x-18\\ &=&(x-2)(x+9) \end{eqnarray}因数分解は高校数学でも使う基本動作なので、反復して速度を上げておきましょう。
(イ)二次方程式の解を求める問題です。(93.9%)
解の公式と平方完成の二つの答案を挙げておきます。
どちらも素早くできるように練習しておきましょう。
一つの問題に複数のアプローチが出来るようにしておくことは、名門公立高校への一歩です。
\begin{eqnarray} 解の公式利用 \\ x^2-3x+1=0 \end{eqnarray} \begin{eqnarray} x &=& \frac{-(-3)\pm \sqrt{(-3)^2-4 \times 1 \times 1}}{2} \\ &=& \frac{3\pm\sqrt{9-4}}{2} \\ &=& \frac{3\pm\sqrt{5}}{2} \end{eqnarray} \begin{eqnarray} 平方完成利用 \\ x^2-3x+1&=&0 \\ x^2-3x&=&-1 \\ x^2-2\times\frac{3}{2}x&=&-1 \\ x^2-2\times\frac{3}{2}x+(\frac{3}{2})^2&=&-1+(\frac{3}{2})^2 \\ (x-\frac{3}{2})^2&=&-\frac{4}{4}+\frac{9}{4} \\ x-\frac{3}{2}&=&\pm\sqrt{\frac{5}{4}} \\ x&=&\frac{3}{2}\pm\frac{\sqrt{5}}{2} \\ x&=&\frac{3\pm\sqrt{5}}{2} \end{eqnarray}(ウ)二次関数の変化の割合問題です。(85.2%)
この問題を取るために必ずグラフを書く癖をつけましょう。
二次関数のグラフは、\(y=ax^2\)の\(a\)が正と負で、変化の様子が違います。
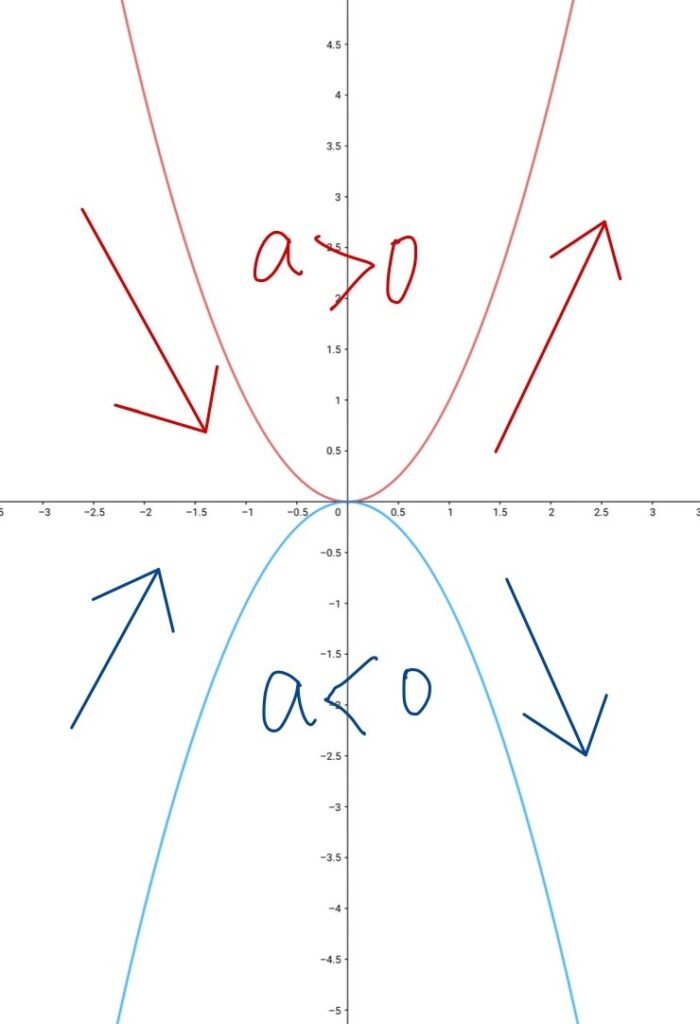
この様にグラフを描くことで、視覚的に増減関係を把握できます。
今回は「xの値が1から4まで増加するときの変化の割合が-3」という条件です。
xが正でグラフが下がっていることを示すので、上記の青いグラフ右側が該当します。
a<0ということを確認して計算に入ります。
これで万が一の時の符号ミスを防げます。
上位高校進学のための入試ではミスをしないための動作が重要です。
もちろん、このグラフをいつでも脳内で即再生できる自信があれば、書かずともよいです。
でもまずは、フリーハンドで素早くグラフを描く訓練をしましょう。
\[y=ax^2\] \begin{array}{c|ccc} y & a & → & 16a \\ \hline x & 1 & → & 4 \\ \end{array} \begin{eqnarray} 変化の割合&=&\frac{yの増加量}{xの増加量} \\ -3&=&\frac{16a-a}{4-1} \\ -3&=&\frac{15a}{3} \\ -3&=&5a\\ a&=&-\frac{3}{5} \end{eqnarray}(エ)一次不等式の文章題です。(80.0%)
文章を読んでそれを式にする問題ですが、これが20%も不正解を生んでいるというのは恐ろしいです。
加減乗除の関係や大小関係を日本語から理解できていないということです。
つまり普段の数学の学習で「何となく」「雰囲気で」問題を眺めているわけです。
今回のカギはズバリ一言「荷物全体の重さが200kg以上」が理解できるか/できないかです。
選択肢4つが不等号・等不等号の違いしかないからです。
流石に荷物全体の重さが分からない人はいないだろうということでしょう。
不等式問題ではどちらかと言えば、乗法だけではなく除法を使ったものが入試では問われます。
そうでない分でも、簡単です。
話を戻して以上以下について簡単に復習しておきます。
\begin{eqnarray} AはB以上\equiv A \geq B\equiv Aは大なりイコールB\\ AはBより大きい\equiv A\gt BA\equiv Aは大なりB\\ AはB以下\equiv A\leq B\equiv Aは小なりイコールB\\ AはBより小さい・B未満\equiv A\lt B\equiv Aは小なりB\\ \end{eqnarray}日常会話レベルの内容ですので、今日覚えて一生忘れないでください。
(オ)平方数に関する問題です。(86.2%)
分数が自然数となるならば、「約分できること」「約分後に分子・分母に平方数(自然数の二乗)が残ること」が条件です。
平方数は最低14までは暗記しておきましょう。
\begin{array}{c|c|c|c|c} 1^2=1 & 2^2=4 & 3^2=9 & 4^2=16 & 5^2=25 \\ \hline 6^2=36 & 7^2=49 & 8^2=64 & 9^2=81 & 10^2=100 \\ \hline 11^2=121 & 12^2=144 & 13^2=169 & 14^2=196 & 15^2=225 \\ \end{array}15以上のx5の平方については、以下の記事を参照してください。
約分するためには素因数分解が便利です。
素因数分解のコツは以下のページを参照して下さい。
今回の分子である540を素因数分解すると\(540=2^2\times3^3\times5\)となります。
これを分子として\(n\)で約分して平方数を残すには、最小で\(n=3\times5\)であれば良いです。
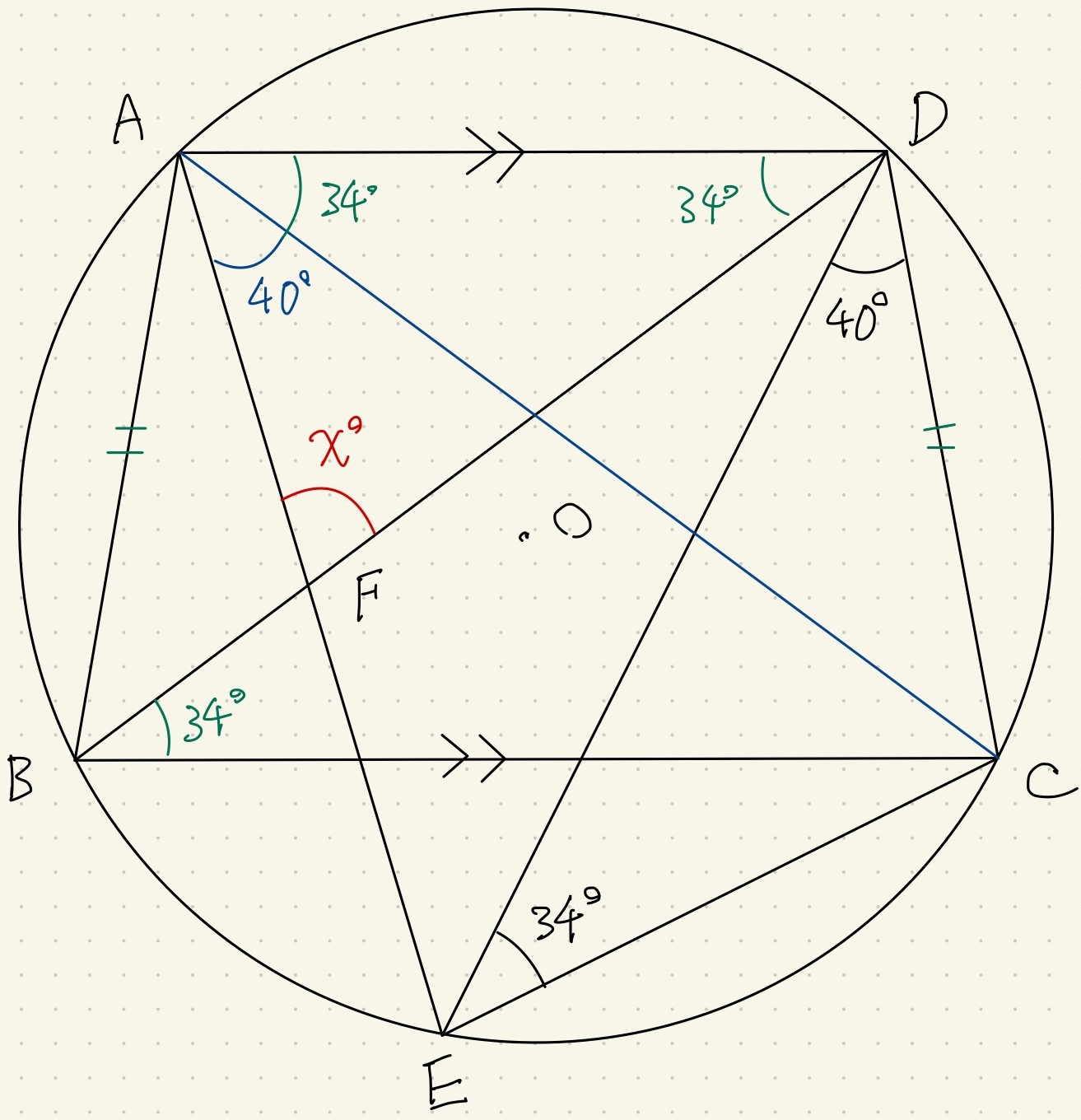
\begin{eqnarray} \sqrt \frac{540}{n}&=&\sqrt \frac{2^2\times3^3\times5}{n}\\ &=&\sqrt \frac{2^2\times3^3\times5}{3\times5}\\ &=&\sqrt 2^2\times3^2\\ &=&6\\ よってn&=&15 \end{eqnarray}(カ)円内の角度に関する問題です。(46.8%)
この手の問題での注意事項は以下の通りです。
- 同じ大きさの弧があれば円周角をチェック。
- 円周角があれば中心角、中心角があれば円周角をチェック。
- 直径があれば円周角=90°。
- 半径が2本で二等辺三角形が作れる。
- 並行な線分があれば錯角をまず疑う。
- 円に内接する四角形の対角和=180°
神奈川県の公立高校入試問題でまず疑うのはこのあたりです。
今回はまず、円周角を利用するために青の補助線を引きました。
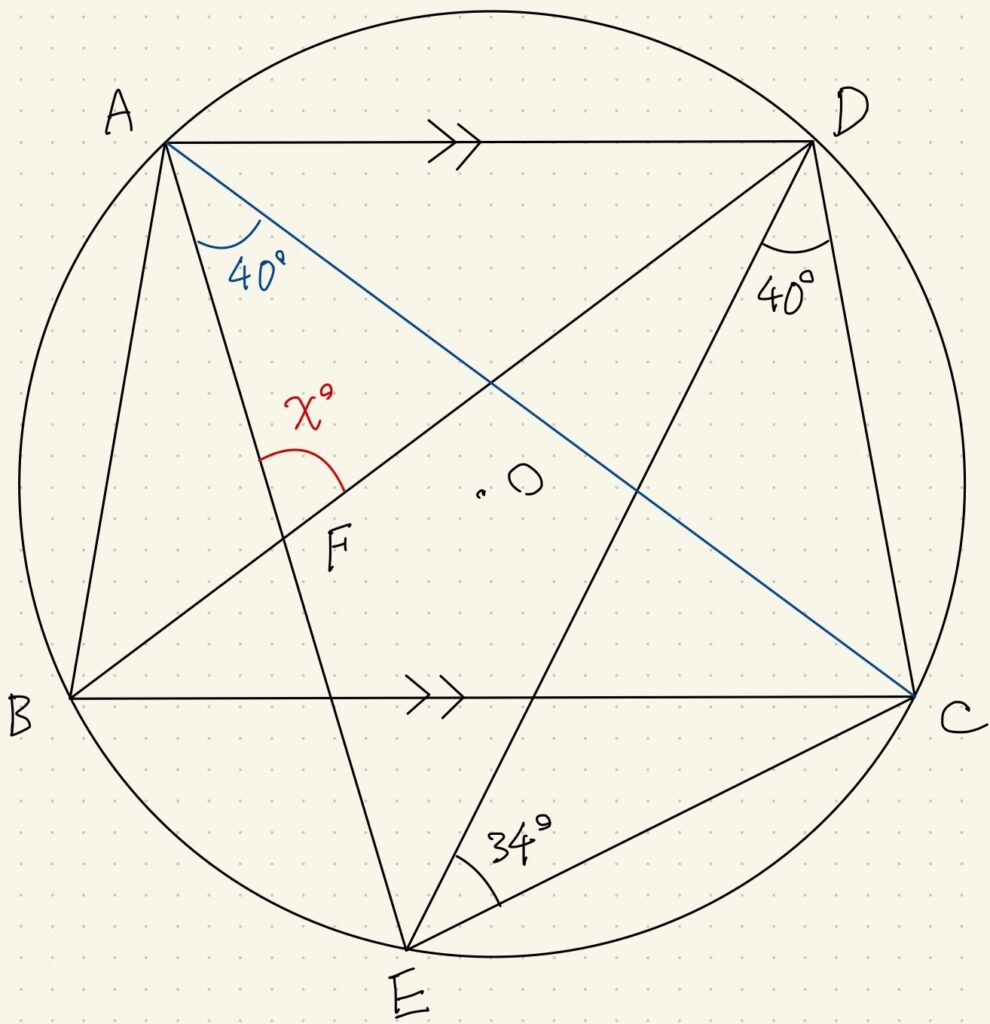
これによって\(\angle EDC=\angle EAC=40^{\circ}\)となります。
同様に円周角を考えて、\(\angle CED=34^{\circ}\)よりこのようになります。
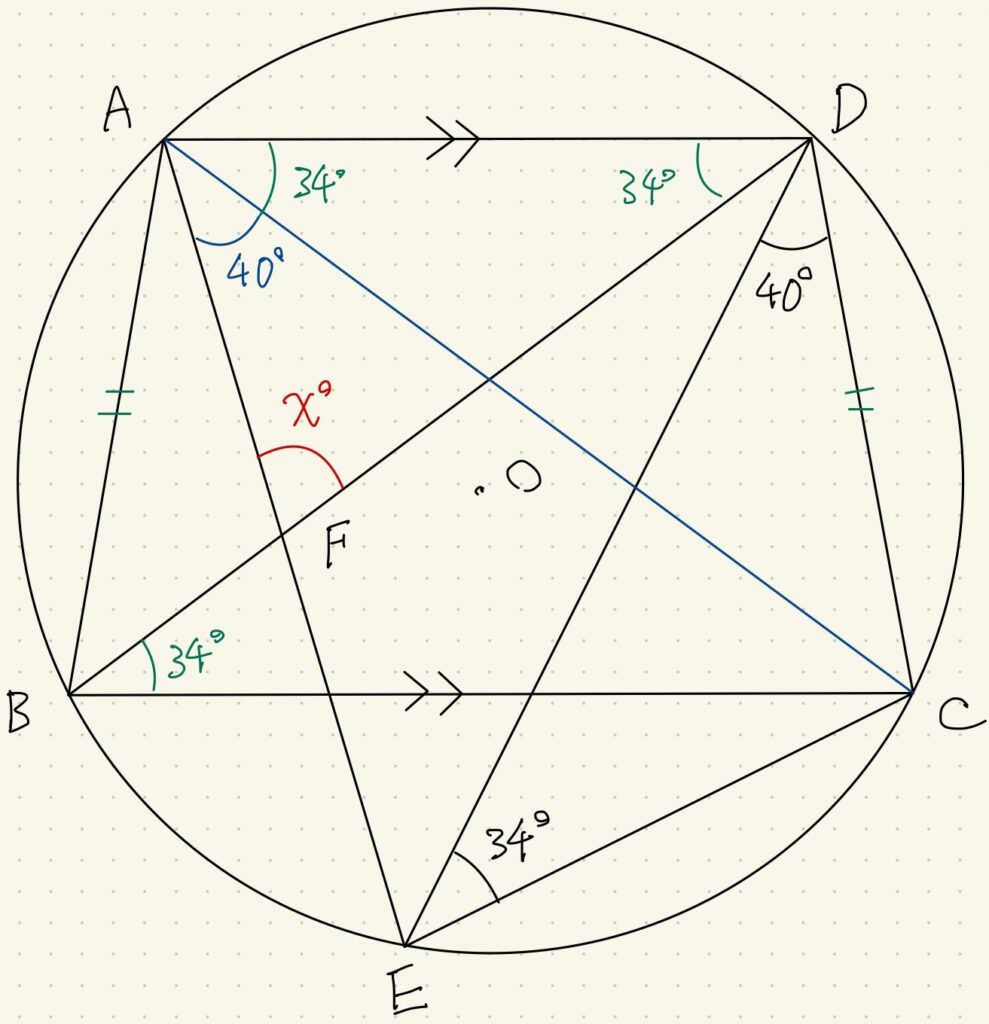
\(\angle CED=\angle CBD=\angle CAD=\angle BDA=34^{\circ}\)です。
最後の部分は\(AD/\!/BC\)より、四角形ADBCが等脚台形であることがヒントです。
等脚台形は左右対称になりますので、\(AB=DC\)が成立し、同じ長さの弦に立つ円周角が等しいことに注目します。
三角形の内角和から\(x^{\circ}=180^{\circ}-40^{\circ}-34^{\circ}-34^{\circ}=72^{\circ}\)です。
問2の総評としては、特に問題のない難度であったと言えます。
最後の一問は正解率が半分ですが、相模原高校・相模原弥栄高校・麻溝台高校進学を目指すなら全問正解すべきレベルです。
問3
(ア)(i)合同証明問題です。(a)(88.2%)(b)(88.7%)
神奈川県の証明問題は昨今空欄補充選択問題ですので、難度は高くありません。
(a)は\(AF=CA-(a)\)とありますので、図を見てなぞれば\(CF\)なのは一目瞭然です。
(b)も同様に\(CE=(b)-BE\)とありますので、\(CB\)です。
これらの問題を間違えたならば、公立上位高校進学への大きなマイナスです。
とにかく図を見て丁寧になぞりましょう。
(ii)線分の長さを求める問題です。(7.8%)
この年の4大失点問題の一つです。
まずは図に求める長さをxとして記入してみます。
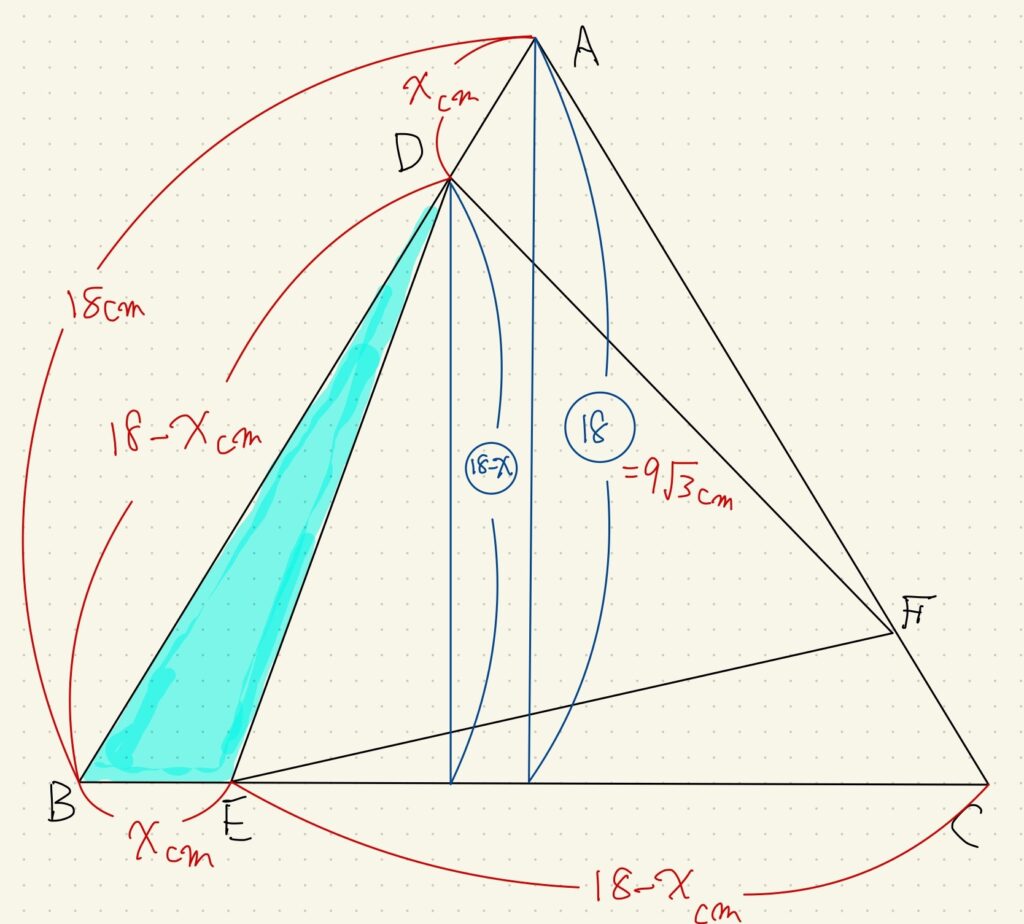
大きい正三角形から、青い部分の小さな三角形を3つ外すと小さい正三角形が残る図形です。
小さい正三角形の一片の長さのヒントが無いので、この青い部分の面積を考えます。
底辺\(xcm\)が分かるので高さが分かれば式が書けそうです。
このとき\(辺AD=xcm\)と\(辺DB=18-xcm\)の比より、\(\triangle ABC と \triangle DBE\)の高さの比が分かります。
三平方の定理で出した\(\triangle ABC\)の高さ\(9\sqrt 3\)cmより、\(\triangle DBE\)の高さは以下のようになります。
\[\frac{18-x}{18}\times9\sqrt 3cm\]
\(\triangle ABC と \triangle DBE\)の面積比は\(12:\frac{5}{3}=36:5\)ですから、これを使って以下の比例式となります。
\begin{eqnarray} 36:5&=&18\times9\sqrt 3\times\frac{1}{2}:x\times \frac{18-x}{18}\times9\sqrt 3\times\frac{1}{2}\\ 36:5&=&18:x\times \frac{18-x}{18}\\ 36:5&=&36:x\times \frac{18-x}{18}\times 2\\ 5&=&x\times \frac{18-x}{9}\\ 45&=&x(18-x)\\ x^2-18x+45&=&0\\ (x-3)(x-15)&=&0\\ x&=&3,15\\ \end{eqnarray}\(AD\lt BD\)という条件から答えは3cmです。
(イ)資料の分析問題です。(32.9%)
資料の分析問題というと度数分布表や箱ひげ図が人気ですが、2021年度は折れ線グラフでした。
相模原高校・相模原弥栄高校・麻溝台高校合格のために差がつく問題です。
「あ」は中央値について考える問題です。
相対度数が分かるので、相対度数×総数で度数が分かります。
この問題を解きながら度数を書き込んでいくと後に使いやすいです。
度数の和を取ると、A中学校の中央値(75・76番目)とB中学校の中央値(50・51番目)がどちらも20m以上25m未満にあると分かります。
「い」は20m未満の生徒の「割合」です。
20m未満までの相対度数の和を比較するとA中学校が0.33、B中学校が0.38となります。
「う」は記録が20m以上25m未満の生徒の人数=度数です。
先ほど度数を記入していればA中学校が24人、B中学校が36人だと分かります。
「え」最後も人数=度数の問題ですので、該当範囲の比較をします。
A中学校は30m以上が17人で25m以上30m未満が26人、B中学校はそれぞれ30人と27人ですから、B中学校は条件に反します。
以上から、「あ・う」の二つが正解だと分かります。
用語と概念さえ覚えておけば後は算数で正解できます。
徹底的に基礎問題を演習して準備しましょう。
(ウ)変化する一次関数の問題です。(i)(52.3%)(ii)(62.9%)
毎秒\(200㎝^3\)で水が増えるので、初期底面積\(40cm\times30cm=1200cm^2\)を考えると、毎秒\(\frac{1}{6}cm}ずつ水位が上がります。
(i)このことから、\(18cm\)上昇するのにかかる時間は\(18\div\frac{1}{6}=108\)秒です。
(ii)(i)より、適するグラフは「3」「4」のいずれかであると分かります。
ここで真面目に向かって右側の水槽を満たすのにかかる時間を計算してもいいです。
しかし、水槽仕切られた左右の幅を比較しましょう。
左が\(40cm\)、右が\(20cm\)です。
ということは、「左の水槽に水が溜まった時間の半分で右の水槽に水が溜まる」のです。
これさえ頭に入れてグラフを眺めれば即「3」が正解だと分かります。
名門公立高校合格のためには観察眼と推論をフル活用していきましょう。
ただでさえ神奈川県の公立高校入試は時間との勝負ですからね。
(エ)連立方程式の問題です。(33.1%)
たかが連立方程式に苦戦した生徒が7割弱いるとは恐ろしい話です。
多くの生徒が中2の学習がロクに出来ていないということです。
これは「中3になってから・部活動を引退してから学習に本腰をいれる」という人間の多さもえいきょうしています。
いうことは、上位公立高校への進学のためにはそこを先んじればよいということです。
設定どおり「先週の大人の利用者数=x人」「先週の子どもの利用者数=y人」とします。
問題文から「大人が1割増加→\(\frac{1}{10}x\)人増加」「子どもが3割増加→\(\frac{3}{10}y\)人増加」となります。
これを使えば(i)は「\(\frac{1}{10}x+\frac{3}{10}y\)」です。
連立方程式は以下の通りに解けます。
\begin{eqnarray} \left\{ \begin{array}{l} x + y = 580 \\ \frac{1}{10}x + \frac{3}{10}y = 92 \end{array} \right. \left\{ \begin{array}{l} x + y = 580 \\ x + 3y = 920 \end{array} \right. 下の式から上の式を辺々引いて\\ 2y&=&340\\ y&=&170 上の式に代入して\\ x+170&=&580\\ x&=&410\\ 今週は1割増加しているので\\ 410+41=451 \end{eqnarray}方程式を解いてホッとして、410と書いてしまうと問題文を読んでいないと言えます。
何を問われているかを確認しておけば「今週の大人の人数」ですから、上のようになります。
問3の総評としては(ア)(ii)以外は確実に得点すべき領域でした。
中2の学習範囲でこれだけ得点できる分野があるのですから、早くから準備しましょう。
問4
いつもの二次関数問題です。
最初に問題文を読んで、分かる点の座標をガンガン書いていきましょう。
点Aはx座標-5ですから直線①\(y=-x\)の式に代入して\(点A(-5,5)\)です。
これを使ってy軸に対称な\(点B(5,5)\)、点A・Bと同じy座標を持つ点Cはy座標が5、線分ABを\(3:2\)に分けるのでx座標も分かり、\(点C(\frac{5}{3},5)\)を書きこみます。
\(AO:OD=5:3\)ですから座標を検討すれば\(点D(3,-3)\)です。
点Eは点Dとy軸対称ですから、\(点E(-3,-3)\)も分かります。
ここまで記入を終えた後に、設問です。
(ア)点Aの座標を使って秒殺です。(85.5%)
\begin{eqnarray} y=ax^2 \\ A(-5,5)を代入して \\ 6=25a \\ \frac{1}{5}=a \end{eqnarray}(イ)点Cと点Eの座標を使って秒殺です。(46.5%)
おなじみの連立方程式で関数式を出しても良いですが、以下の公式を証明できるようにして覚えておくと少し楽に解けます。
\begin{eqnarray} a≠cである2点(a,b)(c,d)を通る直線 \\ y-b=\frac{d-b}{c-a}(x-a) \end{eqnarray}繰り返しますが、証明できるようにしてから使うものです。
暗記して代入するだけなら連立方程式でやってください。
実際に使うと、下の様になります。
\begin{eqnarray} C(\frac{5}{3},5)E(-3,-3)\\ y-(-3)=\frac{-3-5}{-3-\frac{5}{3}}\{x-(-3)\}\\ y=\frac{8}{3+\frac{5}{3}}(x+3)-3\\ y=\frac{24}{9+5}(x+3)-3\\ y=\frac{12}{7}x+\frac{36}{7}-\frac{21}{7} y=\frac{12}{7}x+\frac{15}{7} \end{eqnarray}あっという間に正解まで行けます。
(ウ)神奈川名物・関数の面積比問題です。(5.6%)
2021年の4大失点問題の2つ目です。
偏差値55までの高校なら正解せずとも合格点になります。
正解率は例年低いので、苦手な人は問題を確認する前にパスでも構いません。
しかし、理系大学進学を望むならこの程度の壁は乗り越えていきましょう。
三角形AEC と四角形BCEFの面積が等しいという条件です。
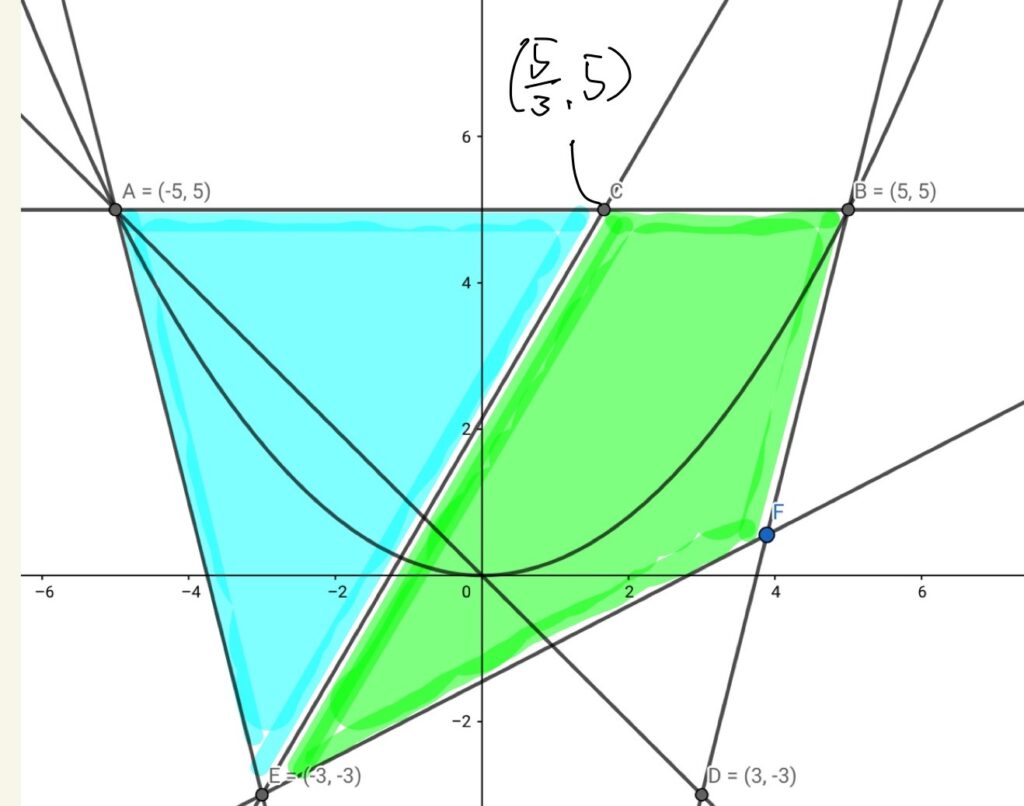
しかし、後者の形が面積を求めにくいです。
これは形を上手く操作して、AEC+BCEFの二等分線となる直線ECというイメージにできれば楽です。
そのためには等積変形が王道です。
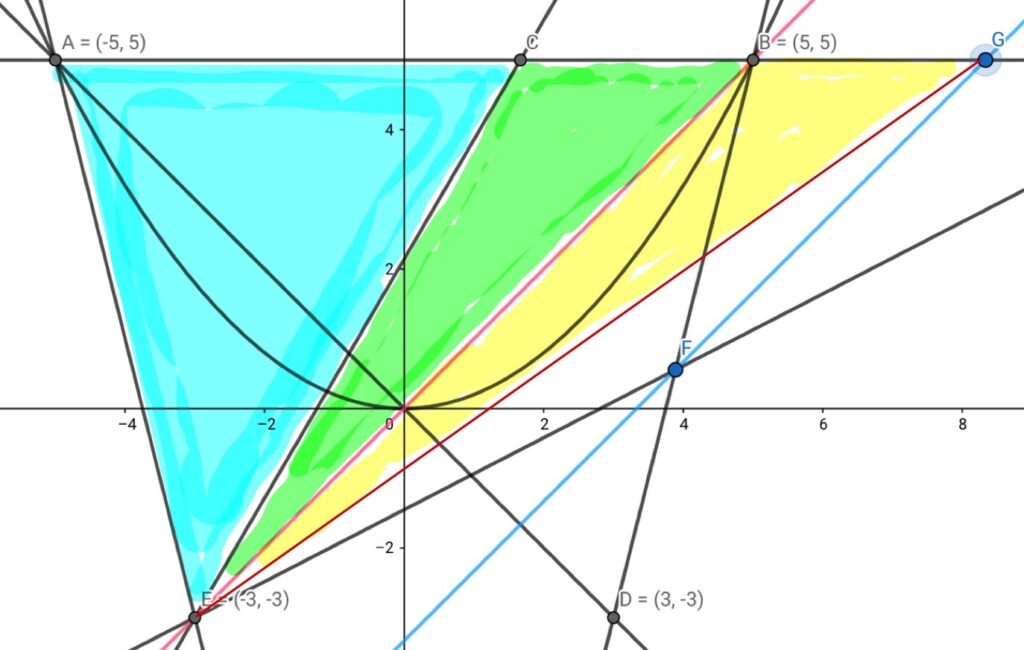
緑の四角形を分割して\(\triangle BCE\)と\( \triangle BEF\)にします。
後者を\(点F\)を通って\(BE\)に平行な直線と\(y-5\)の交点Gで出来る\(\triangle BEG\)は\(\triangle BEF\)と等積です。
このGは、高さの同じ三角形が面積が等しいとなるための底辺から\(AC=CG\)を満たすので\(G(\frac{25}{3},5)\)と求められます。
等積変形の手法から\(BE\)に平行な直線は傾き1となるので、直線FGの式は\(y=x-\frac{10}{3}\)です。
これと\(AD:y=-4x-15\)との交点が\(F(\frac{35}{9},\frac{9}{5})\)です。
問4の総評としては、(ア)(イ)は例年通り確実にとりたい問題、(ウ)は分数計算に粘り強く対応できるかがカギとなる出題でした。
問5
おなじみ確率の問題です。
神奈川県の県立高校入試の確率問題は「きっちり具体例を書け!さもなくば滅びよ!」です。
ということで今回もガチっと書いていきます。
まずは今回の事象について表にします。
\begin{eqnarray} \begin{array}{c|c|c|c|c|c|c} \hline 大&1&2&3&4&5&6\\ \hline P→Q&1&2&1,2&4&1,4&2,4\\ \hline 小&1&2&3&4&5&6\\ \hline Q→R&1&1,2&1,3&1,2,4&1,5&1,2,3,6\\ \hline \end{array} \end{eqnarray}ここを確認しながら問題を解いて漏れを防ぎます。
入試本番でも、必ず表にして書きましょう。
(ア)確率の基本問題です。(44.5%)
「箱Rに入っているカードが4枚」となるためには、b=6しかありません。
その際Qに「1,2,3,6」が無いといけないので、不足している「1,2」をPから移す必要があります。
それはa=3が出た時だけです。
これが全部上の表から分かりますね。
よって確率は\(\frac{1}{36}\)です。
(イ)確率の標準問題です。(11.9%)
4大失点問題の3つ目です。
「箱Rに入っているカードが1枚」を満たすように丁寧に場合分けします。
箱Q「3,5,6」がいつもあるので、b=6が出ると「3,6」の2枚が移動してアウトです。
よって最大でも確認するのは30通りまでです。
a=1のときQは「1,3,5,6」だからb=1で1、b=2で1、b=4で1がRへ。
a=2のときQは「2,3,5,6」だからb=2で2、b=3で3、b=5で5がRへ。
a=3のときQは「1,2,3,5,6」だからb=1で1、b=4で1がRへ。
a=4のときQは「3,4,5,6」だからb=3で3、b=4で4、b=5で5がRへ。
a=5のときQは「1,3,4,5,6」だからb=1で1、b=2で1がRへ。
a=6のときQは「2,3,4,5,6」だからb=2で2、b=3で3、b=5で5がRへ。
合計16通りなので、求める確率は\(\frac{16}{36}=\frac{4}{9}\)。
問5の総評としては、確率の問題は丁寧に数え上げる練習さえしておけば得点源だと言えます。
数学が苦手な人ほど、確率の数え上げは練習しておきましょう。
問6
(ア)立体の体積を求める問題です。(69.1%)
円錐が課題なので、\(錐の体積=底面積\times 高さ\times \frac{1}{3}\)を使います。
底面直径が分かっているので半径は\(3cm\)です。
母線と底面半径を使えば、高さは三平方の定理ですぐに出せます。
\begin{eqnarray} 底面半径3cm、母線9cmの円錐の高さはhについて\\ h^2&=&9^2-3^2\\ h&=&\sqrt 72\\ h&=&6\sqrt 2\\ 円錐の体積&=&\pi \times r^2\times h\times \frac{1}{3}\\ &=&\pi \times 3^2 \times 6\sqrt 2 \times \frac{1}{3}\\ &=&18\sqrt 2 \pi cm^3\\ \end{eqnarray}(イ)立体の表面積を求める問題です。(63.6%)
表面積は展開図の面積で考えます。
円錐は展開すると側面の扇形と底面の円となります。
この時母線の半径Rと底面半径r、扇形の中心角aについては以下の関係があります。
\[\frac{r}{R}=\frac{a}{360^{\circ}}\]
これは「底面の円周=側面の扇形の弧」から導出できるので、書いて理解しておきましょう。
公式として覚えて代入するだけの学習は絶対にしないでください。
今回はこれを使って以下のように求められます。
\begin{eqnarray} 円錐の表面積&=&側面の扇形の面積+底面積\\ &=&\pi R^2\times \frac{a}{360^{\circ}}+\pi r^2\\ &=&\pi R^2\times\frac{r}{R}+ \pi r^2\\ &=&\pi Rr+ \pi r^2\\ &=&\pi r(R+r)\\ &=&\pi \times 3(9+3)\\ &=&36\pi cm^2 \end{eqnarray}(ウ)線分の長さを求める問題です。(3.4%)
4大失点問題のラスボスです。
2021年度もこの問題は、ほぼ合否には影響しません。
まずは他の問題を確実に正解できる力を身につけましょう。
その上で高校以降で理系難関大学進学を目指す志のある生徒諸君はチャレンジです。
と言っても実は、正解率程に難しい問題ではありません。
ここに来るまでに時間を残していれば、十分に解ける問題です。
つまり、「遅いことによって失点」している可能性が大いにあります。
まず点Dの位置を確定します。
展開図を考えるとABは直径ですから、CAとCBを両端とする扇形は全体の半分の中心角を持ちます。
(イ)で見た計算から\(\frac{3}{9}=\frac{a}{360^{\circ}}\)より\(a=120^{\circ}\)です。
その半分の\(60^{\circ}\)で図を描くと、Dはこの位置にあります。
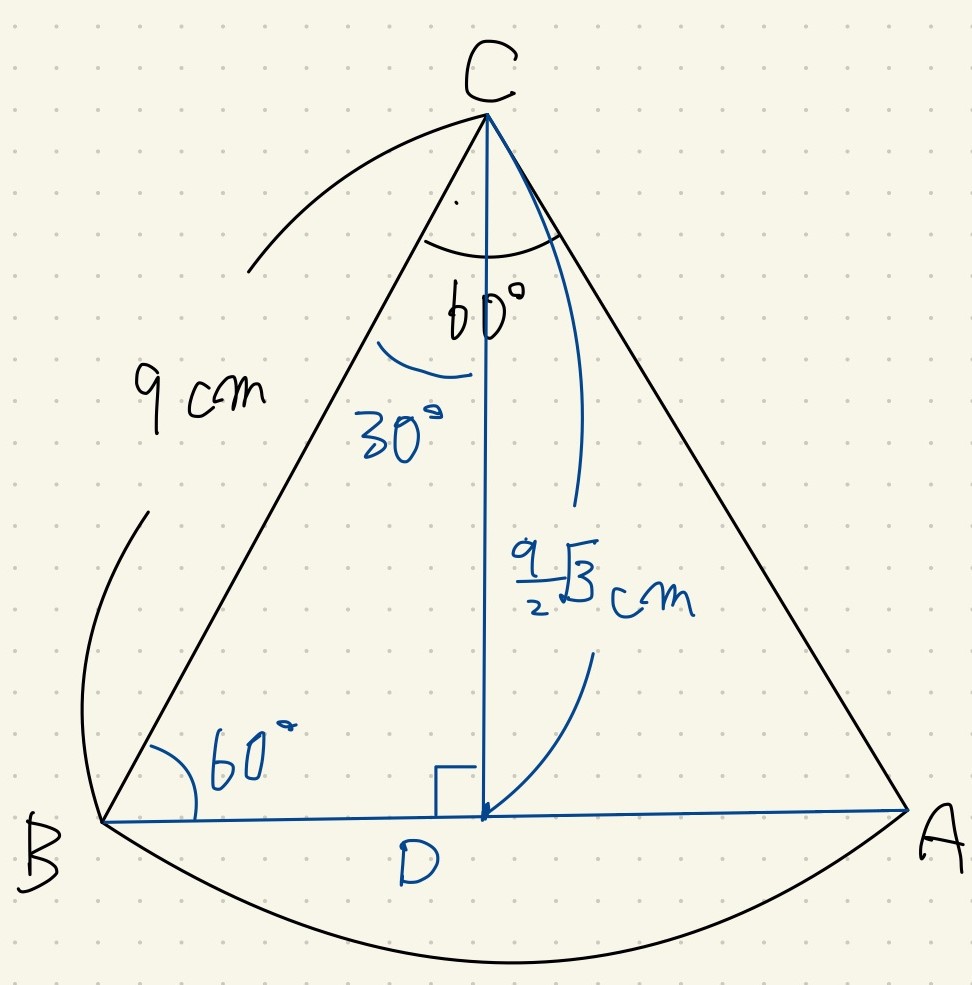
ABの中間地点である点Dは、\(\triangle CAD \)で\(\angle D =90^{circ}\)の直角三角形となります。
図より他の二角もすぐに\(30^{\circ}\)、\(60^{\circ}\)確認できるので、三平方の定理ですぐに\(CD=\frac{9}{2}\sqrt 3 cm\)が出ます。
これをもとに、Dが演習の側面を最短距離で1周する図を描いてみます。
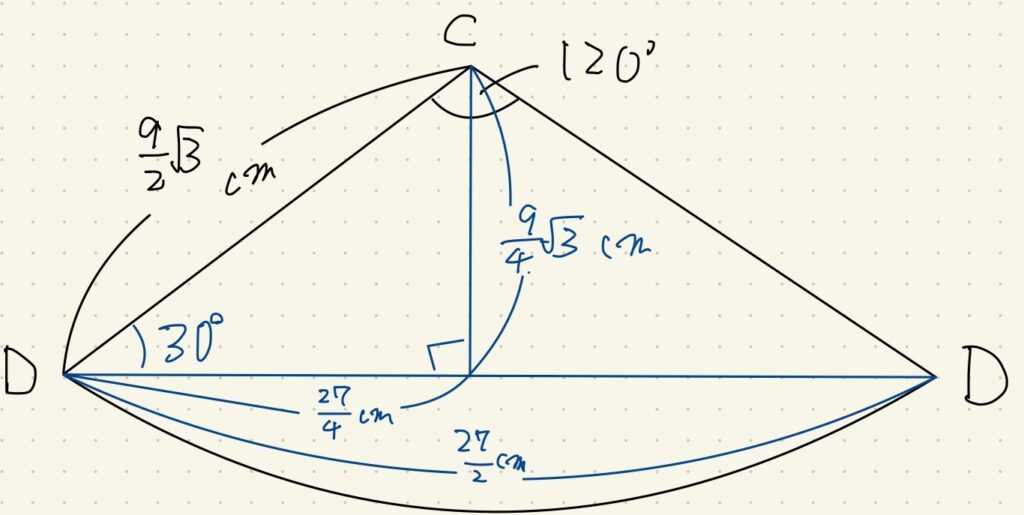
こんどは扇形全体の\(120^{\circ}\)となります。
これも垂線を下せば\(30^{\circ}\)、\(60^{\circ}\)が確認できるので三平方の定理で決着です。
上述の通り、大した問題ではありませんでした。
しかし、ここまでたどり着く速度と集中力次第では失点もあります。
全体講評
2021年は出題範囲の狭さを計算・手数の面倒さで補った出題だったと言えます。
無論100点でなくとも県立相模原高校などに合格は出来ます。
しかしこの問題で言えば、4大失点問題をどこまでくらいつくかは高校進学後の学力のベース判定ともなります。
まずは問題の対応速度を上げる意識で日常の演習を進めましょう。
正解率が低く見えても、法外な難問とは限らないのです。
名門公立高校が君を待っています。