計算のコツと学力が伸びない理由

目次
数学が得意になるために大事なことは
数学が得意になるために大事なことは、概念理解と計算力の強化です。
この二つは並行して進めていかなければいけません。
ここでいう計算力の強化に最適なタイミングは、1学期の学習です。
どの学年でも、1学期に数式計算の学習を行います。
これは、新たに習得して欲しい計算力を最初に養うことで、その学年での学習をスムーズに進めるためです。
ということは、計算力強化を十分に行ったかどうかによって1年分の学習の成否に大きな差が生じるということです。
にも拘らず、新学期当初の浮かれた空気のせいか、簡単(にみえる)学習内容のせいか、計算トレーニングをおろそかにする生徒がどれほどいることでしょうか。
結果として足腰を鍛えないまま難度の上がっていく学習内容についていけないで、数学が苦手になっていきます。
計算力が弱いことのデメリットは大きい
そもそも計算力が弱いことにはいくつものデメリットがあります。
楽しくない
そもそも計算が苦手ですから、不正解が多くなります。
解いていて不正解が多いと学習が楽しくないですから、脳は働こうとしません。
そうするとさらに不正解が増えて集中力が落ちて、さらに楽しくないです。
これで学力が伸びたら奇跡というものです。
学習時間が伸びる
計算が苦手な生徒は例外なく計算が遅いです。
遅いということは一定量の学習を終えるまでにかかる時間が伸びます。
結果として他の学習(応用問題や他教科)に取り組むための時間が削られます。
あるいは学習以外の活動に割ける時間も減っていきます。
これを喜ばしく思う人はそう相違ないでしょう。
演習量が減る
学習が遅いということは単位時間あたりに対応できる問題量が減ります。
同じ1時間学習するときに30問解く生徒と20問解く生徒では、間違える数に1.5倍の差があります。
ということは、自分の学力を伸ばすチャンスにも1.5倍の差が生まれるということdす。
数学に限らずどの教科でも言えることですが、間違えた問題・できなかった問題を克服したときにこそ学力が伸びます。
出来る問題を何問解いたところで学力は伸びません。
間違えてナンボ・解きなおしてナンボです。
そのためにはどうしても多くの間違いに出会い、やり直すための演習量が必要です。
学習初心者であればこそ、です。
学力が伸びてくれば、少ない間違いからリカバーする技術が身につきます。
そうすればより「効率よく」学ぶことが出来るようになります。
しかし、十分学力を身に着けるまでは丁寧に解き続けて量を稼いでもらいたいです。
それが出来ないということが、解く速度が遅いことによる演習量不足の最大の問題点です。
計算力を上げる方法
ではその計算力を上げるにはどうしたらいいでしょうか。
まず考えて欲しいことが2つあります。
丁寧に式を書く
計算が上達しない生徒の特長の一つに、式の扱いが雑であることが挙げられます。
自分がこれから計算する式を丁寧に書かず、いきなり筆算します。
計算の途中を示す式を書かずに、無暗に暗算で解こうとします。
あるいはそもそも暗算で済ませられる程度の計算でしか解こうとしないで、長い式を書く問題で手を止めます。
つまるところ実力不足の上に努力不足というわけです。
学習の基本は「出来ることからコツコツとやり続ける」というものです。
一足飛びにやろうとする姿勢は賢くなる姿勢とは程遠いものです。
手を抜くことを習い性としてはいけません。
カッコなども含めて手抜きすることなく丁寧に書きましょう。
その時に、等号の位置なども気を付けて見やすく書きましょう。
筆算を書く場合にも、ノートの余白にコソコソっと書くような姿勢はダメです。
見やすい位置に大きく書きましょう。
そもそも、式を書くというのは頭の負担を減らすための行為です。
全ての計算を脳内で完結させるのは脳に負担がかかりすぎます。
脳という小さな机の上いっぱいにノートや本や辞書を広げようとするようなものです。
それでは考えなければならないことが抜け落ちたり、考える速度が落ちることになります。
狭い机での作業効率が高くはならないというのと同じことです。
計算のコツを増やす
一方で計算を上手くやるには、すべての事柄を式や筆算にしていけばいいというものではありません。
速度を上げて正確性を保つためには、計算のコツとも呼べるものをどれだけ身に着けて使いこなすかも重要です。
その基本となるのは「たして10になる数」や「かけて10/100/1000になる数」の習得があります。
これらを使いこなすようになれば、無駄な筆算を減らせます。
筆算はとても便利なツールですが、頼りすぎると暗算力が確実に落ちます。
ここで言う暗算はあくまで即正解できる手段としてのものです。
暗算の名のもとに答えが出るまで時間をかけて頭の中でやってはいけません。
計算はいかに考えこまない部分を増やすかということが一つのコツになります。
例えば、掛け算九九をいちいち考えて答えを出す人はいないはずです。
もしいたら、今すぐ200回音読して暗記しましょう。
それと同じように、頻出の計算パターンを頭に叩き込んで即引き出せるようにしておきましょう。
それが先ほどの「たして10になる数」や「かけて10/100/1000になる数」のようなものです。
いずれにせよ、いかに「計算しないか」が計算のコツです。
計算のコツの一例・平方数
ここで、計算のコツの一例を出してみます。
計算をしていると同じ数同士の積=平方数が良く出てきます。
これを暗記しておくことは掛け算九九と同様に役立ちます。
その例として「一の位が5の二桁の数の平方数」を考えてみましょう。
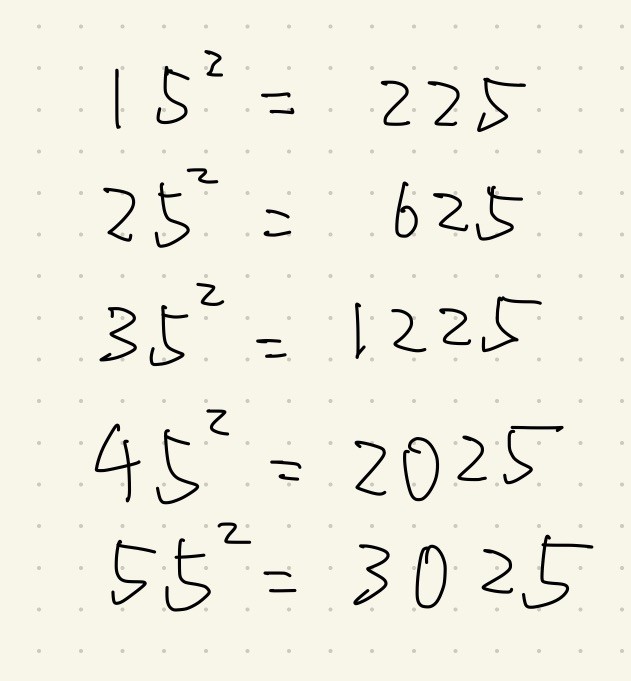
こういうシリーズです。
大抵の中学生はこの計算を筆算することでしょう。
しかし、なるべく筆算をしないことが目標ですから、それ以外の計算でやります。
もちろん、この計算結果を掛け算九九よろしく丸暗記しても構いません。
しかし、丸暗記せずにこれを攻略してこそコツというものでしょう。
この式の列を観察すると、気づくことがあるはずです。
ちょっと考えて、次の画像を見てください。

そう、下二桁・十の位と一の位が全て25です。
これは、元の数の一の位が5であるということが理由です。
これが分かるだけでも、ちょっと計算で頭を使う量が減るのが分かりますよね。
では、百の位と十の位がどうにか出来ればなお良いということです。
再び法則が無いか、考えてから次の画像を見てください。
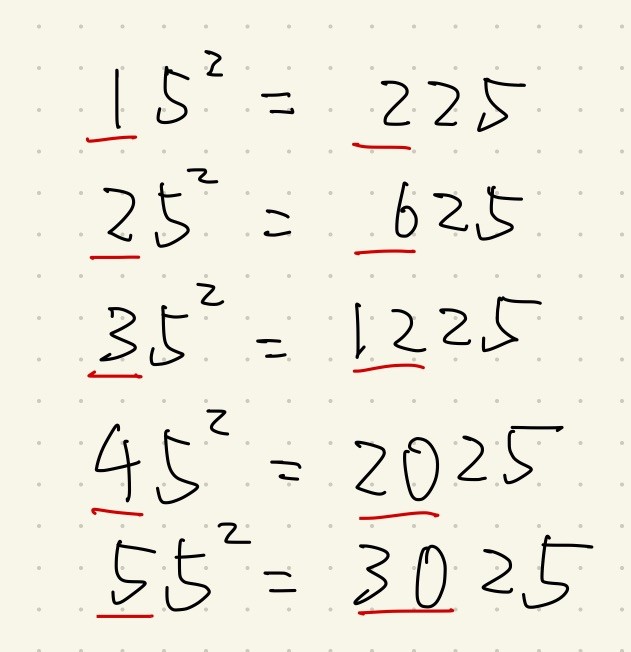
先ほど元の数の一の位に注目したのですから、今度は十の位に注目するのが道理というものです。
左辺と右辺を見比べてみましょう。
クイズか何かだと思ってじっくり観察すると、法則がきっと見えてきます。
ぜひぜひ、じっくり考えてから次の画像を見てください。
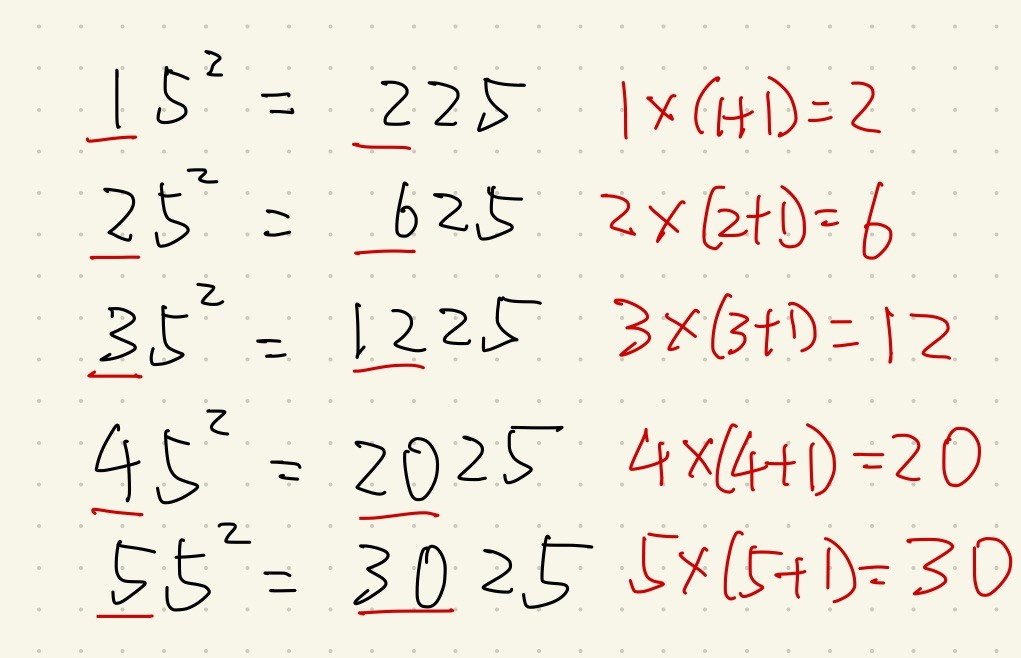
左辺の十の位の数に、その数の次の数をかけたものが右辺の上の位に出ていることが分かります。
そう考えると、左辺を見てから右辺を出すために考えることは次のように言語化・式化できます。

青い文字がこの計算を行うためのコツとなる式です。
実際に頭の中で考えるのは上の二桁のための、一桁の掛け算だけです。
積を書いたら後はほぼ考えずに25と書けば、それで正解です。
これが、なるべく計算しないという行動の意味です。
これをじっくりと見つめて次の例題に挑戦してください。

もちろん、この計算が出題されることを賢明な当ブログ愛読者の皆さんならば想定されていたでしょう。
目標時間は、まずは4問20秒、最終的には10秒以内です。
計算が速すぎて手が追いつかないレベルを目指しましょう。
では、正解です。
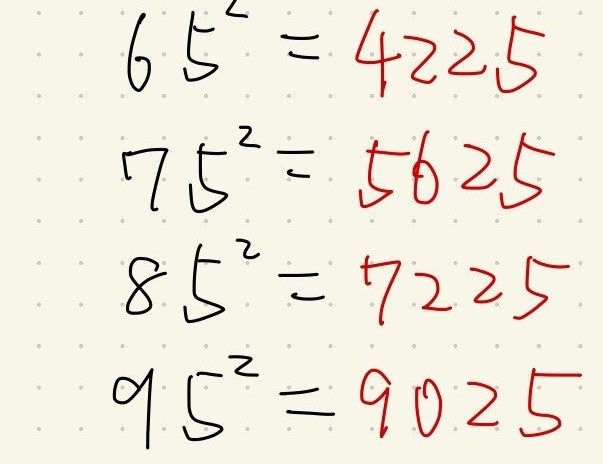
いかがでしょうか。
もちろん正解できましたね。
こういうコツを丁寧に使いこなして、計算量を減らして計算上手になりましょう。
学力が上がらない理由
さて、この記事を読んで「賢くなった!」と思う人もいるでしょう。
それこそが、あなたが賢くならない理由です。
計算のコツであれ解説であれ、世の中にはいろんな参考書・問題集があっていろんなことが書かれています。
あるいはそもそも、学校や塾の講義授業で様々な指導がなされています。
にも拘らず、学力が上がらずに困っている生徒諸君・保護者の皆様がいらっしゃいます。
これはどういうことでしょうか。
理由は単純です。
「定着するまでアウトプットしまくってないから」です。
演習量が絶対的に不足しているんです。
誰かの解説を聞いたり読んだりして、学力がついたつもりになっているだけだからです。
インプットと比してアウトプットの量が足りないのです。
分かりやすく言えば、「やってないから出来ない」ということです。
だから、青木学院では演習授業を大きくとってアウトプットをガンガンやってもらうのです。
大手塾の講義授業には素晴らしいものがたくさんあります。
しかしそこで学力が思うように伸びていないなら、青木学院でガンガン演習してください。
一朝一夕に成果は出ません。
しかし、長く積み上げた努力は必ず生徒諸君の実力となります。
ぜひ、良いインプットを十分な量のアウトプットで実力として、自分の望む自分になってください。