2020年 神奈川県公立高校入試 数学 解説
神奈川県の公立高校を志望する皆さん、神奈川県の過去問を使って力試しをしたい皆さんへ。
今回は2020年度の数学の問題について検討してみましょう。
問題をお持ちでない方は以下のリンクからでも入手できます。
事前に全ての問題に取り組み、自分なりにどこまで考えられたかをまとめてから解説をお読みください。
各小問の出だしには正解率を添えておきます。
問1
(ア)毎年通りの正負の数の加減問題です。(92.8%)
こんな問題は全員正解できる、と思うかもしれません。
しかし(ア)の正解率は92.8%です。
つまり、7.2%は何らかのミスをしています。
ゆめゆめ油断してはいけません。
符号ミスをしていないか、必ずペン先で確認しましょう。
(イ)文字式の除法問題です。(97.4%)
この問題も符号ミスに注意するのが第一です。
その上でお勧めしたいのは「割り算を一度分数にしてみる」表記です。
\begin{eqnarray} 52a^2b \div (-4a) &=& – \frac{52a^2b}{4a} \\ &=& -13ab \end{eqnarray}ここで大事なのは、「必ず最初に符号を決めるクセ」をつけることです。
分母分子を上下に並べて見比べることで約分として処理すれば文字数字のミスも減らせます。
少なくとも暗算でミスをしているのであれば、一度見やすく書くように行動を変えましょう。
(ウ)神奈川典型問題の一つ、平方根入りの加法減法です。(95.5%)
この問題のポイントは「必ず平方根部分が一致する問題である」点です。
どの平方根を軸にするかは、与式の分母部分がヒントになります。
今回の問題では√7がそれです。
分数ではないほうの平方根から√7を取った残りが平方数に必ずなります。
分数の方は有理化を行えば約分できますから、約分後に加法減法を行いましょう。
\begin{eqnarray} \sqrt{28} + \frac{49}{\sqrt{7}} &=& 2\sqrt{7} + \frac{49\sqrt{7}}{7} \\ &=& 2\sqrt{7} +7\sqrt{7} \\ &=& 9\sqrt{7} \end{eqnarray}また、有理化より「平方根で約分」という意識を持つとさらに良いです。
\[49 = 7^2 = 7 \sqrt{7}\sqrt{7}\]このように考えると、下のように書けます。
\begin{eqnarray} \sqrt{28} + \frac{49}{\sqrt{7}} &=& 2\sqrt{7} + \frac{7\sqrt{7}\sqrt{7}}{\sqrt{7}} \\ &=& 2\sqrt{7} +7\sqrt{7} \\ &=& 9\sqrt{7} \end{eqnarray}(エ)文字式分数の加法減法問題です。(85.0%)
要点は通分と符号の分配法則の失点を防ぐことです。
苦手であれば一度必ず途中式に書くこと、分配法則は必ずペン先で数字・文字を指して確認することで対応します。
また、今回の問題で言えば後ろの(カッコ)内の符号が与式では正と負で異なっています。
展開後も符号が異なっていることを確認できれば、ミスを自分で発見できます。
与式で(カッコ)内の符号が同じならば展開しても同じ、異なるなら異なるというリズムです。
\begin{eqnarray} \frac{3x – 4}{3} – \frac{x – 2y}{4} &=& \frac{4(3x – 4) – 3(x – 2y)}{12} \\ &=& \frac{12x – 16y – 3x + 6y}{12} \\ &=& \frac{9x – 10y}{12} \end{eqnarray}(オ)二次式の計算問題です。(91.0%)
大問1でずっとそうであるように、やはり展開時の符号ミスをペン先で確認して防ぎましょう。
これを置き換えずに強引に展開すると下のような答案になります。
\begin{eqnarray} (\sqrt{2} + 1)^2 -5(\sqrt{2} + 1)+4 &=& 2 + 2\sqrt{2} + 1 – 5\sqrt{2} – 5 + 4 \\ &=& 2+1-5+4+2\sqrt{2}-3\sqrt{2} \\ &=& 2 -3\sqrt{2} \end{eqnarray}2020年度の問題では式の一部を文字で置き換えて処理する書き方が一般的です。
\begin{eqnarray} (\sqrt{2} + 1)^2 -5(\sqrt{2} + 1)+4 &=& A^2 – 5A + 4 \\ &=& (A – 1)(A – 4) \\ &=& \{(\sqrt{2} + 1) – 1\}\{(\sqrt{2} + 1) – 4\} \\ &=& \sqrt{2}(\sqrt{2} – 3) \\ &=& 2 -3\sqrt{2} \end{eqnarray}この式の答案、具体的には1行目・2行目・4行目を省略して書けると、上の答案より速くなります。
問1の総評としては、何があってもここまでで失点してはいけないレベルということです。
大学進学を目指す公立高校合格のために、絶対に満点でクリアしましょう。
問2
(ア)連立方程式の基礎問題です。(90.9%)
方程式の解は、元の方程式に代入して等号が成立するものですから、その通りに処理してみればただの連立方程式とみなせます。
\begin{eqnarray} \left\{ \begin{array}{l} ax + by = 10 \\ bx – ay = 5 \end{array} \right. \\ \end{eqnarray} x=2 , y=1 を代入 \\ \begin{eqnarray} 2a + b &=& 10 \tag{1} \\ 2b – a &=& 5 \tag{2} \end{eqnarray} (1)+(2) \times 2より \begin{eqnarray} 5b &=& 20 \\ b &=& 4 \\ \end{eqnarray} (1)に代入して \begin{eqnarray} 2a+4 &=& 10 \\ 2a &=& 6 \\ a &=& 3 \end{eqnarray}ここでは加減法で対応できる問題が多いです。
タイムロスを防ぐためにも地道な計算力トレーニングは欠かさずに行きましょう。
(イ)二次方程式の解を求める問題です。(90.5%)
基本的に解の公式を利用してお終いですが、問題によっては平方完成でも構いません。
どちらも素早くできるように練習しておきましょう。
特に平方完成は、高校数学Iでの二次関数の頂点を求める場面でまた使う技術です。
先を見越して丁寧に解法を増やしましょう。
\begin{eqnarray} 解の公式利用 \\ x^2-5x-3=0 \end{eqnarray} \begin{eqnarray} x &=& \frac{-(-5)\pm \sqrt{(-5)^2-4 \times 1 \times (-3)}}{2} \\ &=& \frac{5\pm\sqrt{25+12}}{2} \\ &=& \frac{5\pm\sqrt{37}}{2} \end{eqnarray} \begin{eqnarray} 平方完成利用 \\ x^2-5x-3&=&0 \\ x^2-5x&=&3 \\ x^2-2\times\frac{5}{2}x&=&3 \\ x^2-2\times\frac{5}{2}x+(\frac{5}{2})^2&=&3+(\frac{5}{2})^2 \\ (x-\frac{5}{2})^2&=&\frac{12}{4}+\frac{25}{4} \\ x-\frac{5}{2}&=&\pm\sqrt{\frac{37}{4}} \\ x&=&\frac{5}{2}\pm\frac{\sqrt{37}}{2} \\ x&=&\frac{5\pm\sqrt{37}}{2} \end{eqnarray}(ウ)二次関数の変化の割合問題です。(83.3%)
この問題を取るために必ずグラフを書く癖をつけましょう。
二次の係数が負なので、上に凸のグラフを描いて座標を書き込みます。
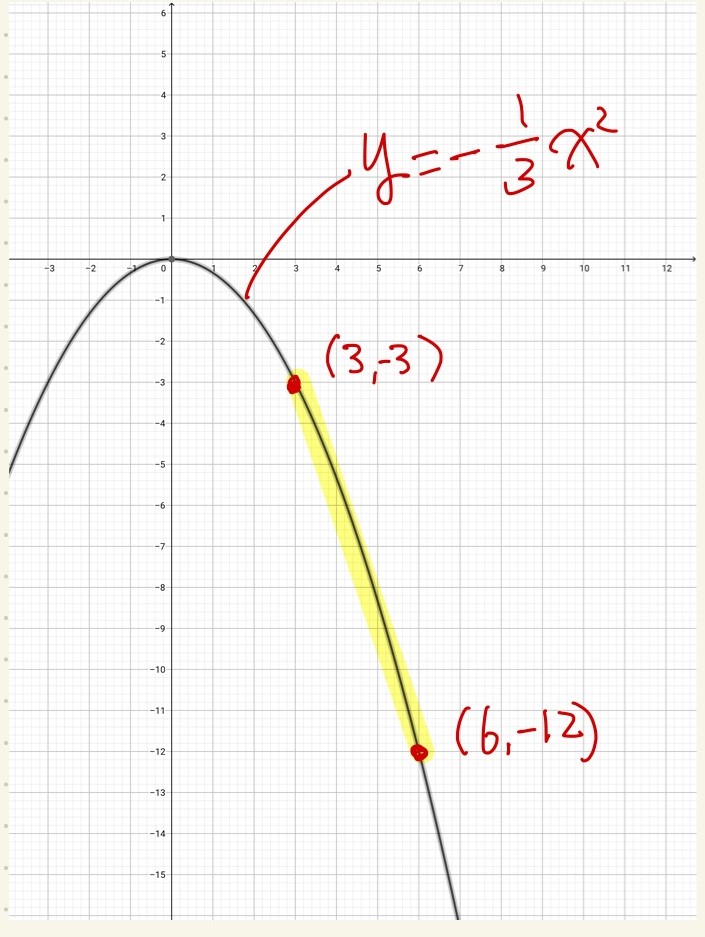
この様にグラフを描くことで、視覚的に大小関係を把握できます。
例えば\((6,-12)\)という座標を\((6,12)\)と書くような事故を防げます。
グラフの見た目から、x座標6の点が下にある、つまり負の数であることが明らかだからです。
また、変化の割合についても視覚的に右下がりの範囲にあるのでマイナスであると一目瞭然です。
選択肢3・4のような正の値は絶対にとらないと分かるはずです。
こういう手順を省略して失点するようなレベルでは論外です。
このようなグラフを描かなくても正解できるというのは事実です。
しかし、グラフを描かないことが習慣になってしまうのは高校数学においてほぼ致命傷です。
目先の一問のために手を抜く姿勢が将来の挫折の種となります。
フリーハンドで素早くグラフを描く訓練をしましょう。
\begin{array}{c|ccc} y & -3 & → & -12 \\ \hline x & 3 & → & 6 \\ \end{array} \begin{eqnarray} 変化の割合&=&\frac{yの増加量}{xの増加量} \\ &=&\frac{-12-(-3)}{6-3} \\ &=&\frac{-9}{3} \\ &=&-3 \end{eqnarray}(エ)一次方程式の文章題です。(82.7%)
この問題は比例式を意識して解きたいところです。
比例式の使いどころは「ある値が2倍、3倍となったときに2倍、3倍と連動する値がある」ときです。
単純に比が出てきていれば比例式が使えるということも言えますが、分かりやすく比の式を見せてもらえなくても比例式が使えるようにします。
今回は子ども1人の入場料を求める問題ですから、これをxとおいて立式します。
(大人1人の入園料):(子ども1人の入園料)=5:2=(x+600):x \begin{eqnarray} 2(x+600)&=&5x\\ 1200&=&3x\\ 400&=&x \end{eqnarray}別解も出しておきます。
比例の問題を解く際には「比と具体的な値が両方分かっているものが必要」ということに注意します。
今回は具体的な値である「大人1人の入園料と子ども1人の入園料の差600円」に該当する比が欲しいです。
これは条件から3であることがすぐに分かります。
\begin{eqnarray} (比の3):600円\\ (比の1):200円\\ (子ども1人の入園料である比の2):400円 \end{eqnarray}方程式で解いて欲しい問題なのでしょうが、こういう見方も押さえておきましょう。
(オ)平方数に関する問題です。(72.3%)
分数が自然数の平方となるならば、「約分できること」「約分後に平方数(自然数の二乗)が残ること」が条件です。
平方数は最低14までは暗記しておきましょう。
\begin{array}{c|c|c|c|c} 1^2=1 & 2^2=4 & 3^2=9 & 4^2=16 & 5^2=25 \\ \hline 6^2=36 & 7^2=49 & 8^2=64 & 9^2=81 & 10^2=100 \\ \hline 11^2=121 & 12^2=144 & 13^2=169 & 14^2=196 & 15^2=225 \\ \end{array}15以上のx5の平方については、以下の記事を参照してください。
約分するためには素因数分解が便利です。
素因数分解のコツは以下のページを参照して下さい。
素因数分解すると\(5880=2^3\times3\times5\times7^2\)となります。
これを分子として\(n\)で約分して平方数を残すには、最小で\(n=2\times3\times5\)であれば良いです。
\begin{eqnarray} \frac{5880}{n}&=&\frac{2^3\times3\times5\times7^2}{2\times3\times5}\\ &=&2^2\times7^2\\ n=30 \end{eqnarray}(カ)円内の角度に関する問題です。(52.5%)
この手の問題での注意事項は以下の通りです。
- 同じ大きさの弧があれば円周角をチェック。
- 円周角があれば中心角、中心角があれば円周角をチェック。
- 直径があれば円周角=90°。
- 半径が2本で二等辺三角形が作れる。
- 並行な線分があれば錯角をまず疑う。
- 円に内接する四角形の対角和=180°
神奈川県の公立高校入試問題でまず疑うのはこのあたりです。
必要な補助線も、これらを意識して引きましょう。
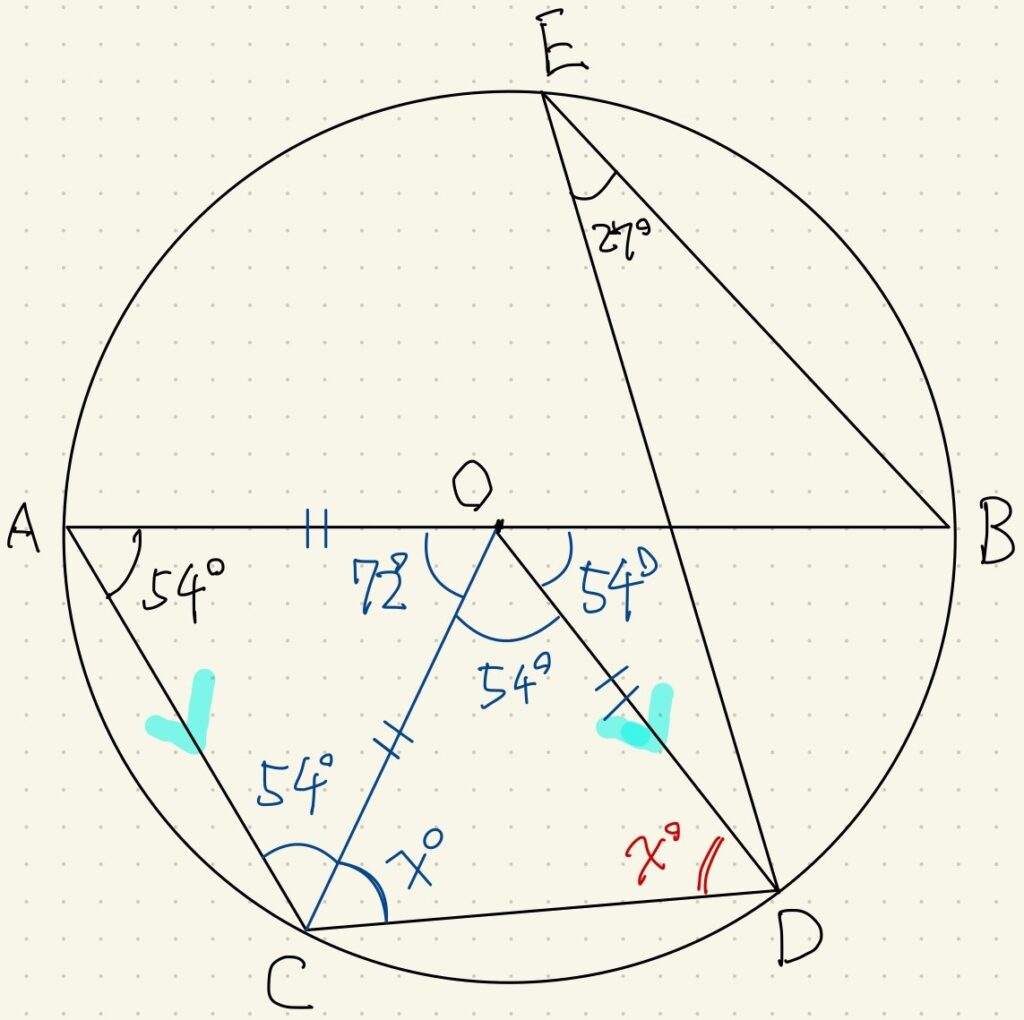
今回は半径を意識して青い補助線を引きました。
円周角\(\angle DEB=27^{\circ}\)より中心角\(\angle DOB=54^{\circ}\)です。
また、補助線OCで三角形OACが\(OA=OC\)の二等辺三角形ですから、頂角\(\angle AOC=72^{\circ}\)が分かります。
直線上の角の和は\(180^{\circ}\)ですから、\(\angle COD=54^{circ}\)となります。
三角形OCDも\(OC=OD\)の二等辺三角形ですから、\(\angle OCD=\angle ODC=63^{\circ}\)です。
また別解として、中心角\(\angle DOB=54^{\circ}\)より\(AC /\!/ OD\)より、錯角を使って\(\angle COD=54^{\circ}\)を宣言してもいいです。
問2の総評としては、特に問題のない難度であったと言えます。
最後の一問は正解率が半分ですが、相模原高校・相模原弥栄高校・麻溝台高校進学を目指すなら全問正解すべきレベルです。
問3
(ア)(i)合同証明問題です。(a)(88.2%)(b)(88.7%)
神奈川県の証明問題は昨今空欄補充選択問題ですので、難度は高くありません。
(a)は次の行に\(\angle ADB=\angle ACB\)とあります。
円周角がの両端を見れば\(\stackrel{\huge\frown}{AB}\)に立っていることが確認できます。
(b)は前の行に\(\angle CBD\)の二等分線と書かれているので、これもすぐに分かります。
この辺りで失点するのは、問題文を読まない、図と見比べないずさんな解き方をしているだけです。
(ii)同一円周上の点問題です。(39.1%)
ここにきて正解率がグッと下がります。
同一円周上にあることを宣言するには、下のいずれかを満たせばよいです。
- 中心からの距離が等しい
- 同じ弧に立つ円周角を持っている
- 4点を結んでできる四角形の対角和が\(180^{\circ}\)
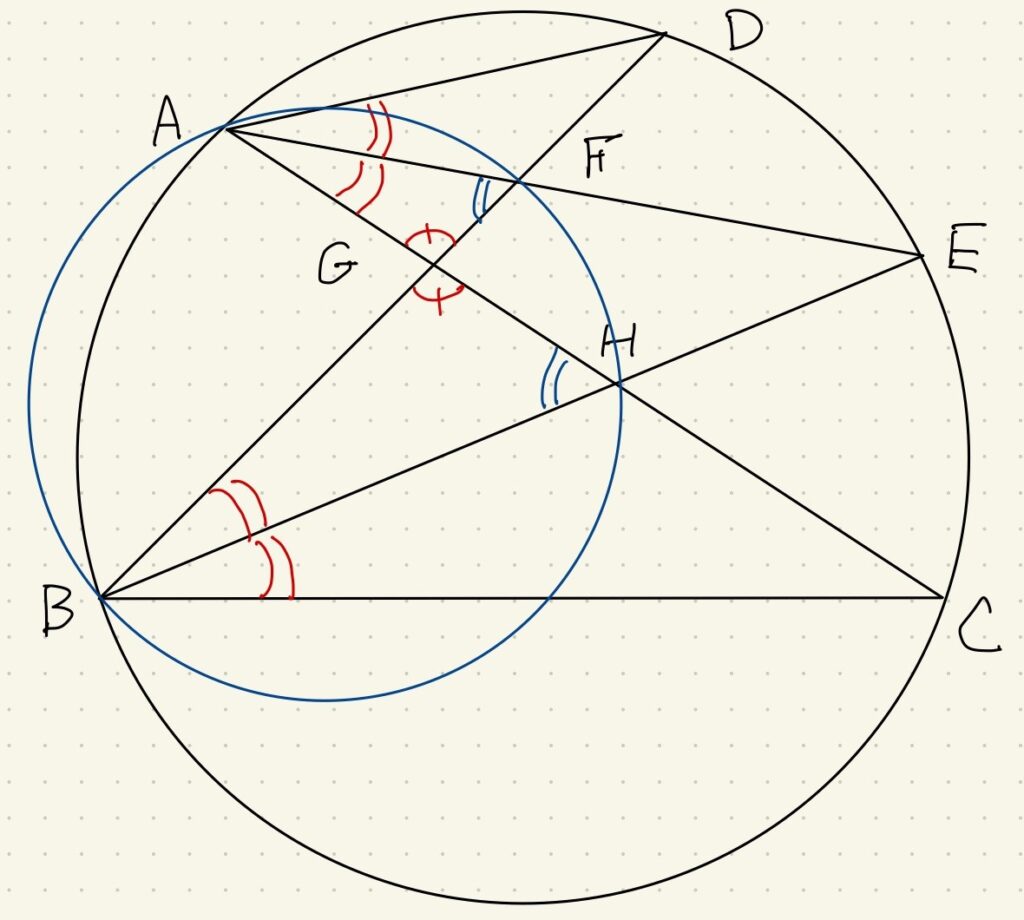
与条件より\(\angle CBD\)の二等分線より\(\angle CBE=\angle DBE\)です。
それぞれの同じ弧に立つ円周角より、\(\angle CBE=\angle CAE=\angle DBE=\angle DAE\)と言えます。
このとき三角形AGFと三角形BGHは対頂角\(\angle AGF=\angle BFH\)を考慮して相似となります。
よって対応する角である\(\angle AFG=\angle BHG\)となります。
ということは、\(\angle AFB=\angle AHB\)が同じ弧に立つ円周角が等しいとみることができます。
よって上の図の青い円に4点ABHFがあると言えます。
この問題見た目でFとHを選ぶことも何となくできます。
正解した受験生の中には、そうして選んだ人もいるでしょう。
丁寧に解けるようにしておきたいです。
(イ)資料の分析問題です。(i)(40.7%)(ii)(54.9%)
ここ数年のトレンドとなっているので、データの比較は迅速に行えるように練習しておきましょう。
相模原高校・相模原弥栄高校・麻溝台高校では合否を分ける問題ともなりえる正解率です。
この問題で絶対にやるべきことは「最初に全部の説明を読んで、どの説明から攻略するかを決める」です。
上から順に馬鹿正直にやっては手間が省けない場合があるので、必ず全部読みましょう。
その上で、「分かりやすい条件から検討する」を徹底してください。
今回で言えば1月についての説明が4つ、11月についての説明が3つ(重複あり)ですから、11月から検討します。
ここで条件をどれから比べるか決めきれない(決断力が無い)状態では敗北です。
日ごろからガンガン意思決定をしていくマインドに自分を強引に変えてください。
さて、今回はまず説明4の「1月、11月ともに、寒暖差が4℃未満の日は4日以内であった」から、A(0日)B(3日)D(4日)E(2日)のみが選択肢になります。
次いで説明5の「11月には寒暖差が2.1℃の日があった」から、11月の候補からAが外れます。
残る説明の中で11月について書かれているのは説明6です。
「11月の寒暖差の最頻値は4℃以上6℃未満の階級の階級値であった」から、Dのみが該当します。
1月の候補はABEの三つになりました。
説明1から「寒暖差が12℃以上の日はなかった」のでAが除外されます。
説明2の中央値は、どちらも同じ位置にありそうですので説明3から検討します。
「平均値が2番目に大きい」のが1月なので、グラフの概況からAの次に平均値が高い、すなわちBEのうち平均値が高いものを選びます。
どちらのグラフも6℃以上8℃未満の数値が中央値を含むので、この左右のバランスを比較します。
すると8℃以上10℃未満の資料数はどちらも8ですが、10℃以上12℃未満の資料数がEが大きいです。
さらに6℃未満の資料数はBが大きいです。
ということは細かく計算せずとも、Eの方が平均値が高いと推定できます。
もちろん、迅速に平均値を計算する計算力があれば申し分なしです。
(ウ)平面図形の面積問題です。(5.1%)
弥栄・麻高に合格するという点だけを考えれば捨て問題と言ってもいいです。
しかし相模原高校に進学するということは上位7%以上の学力を備えるということです。
正解率5.1%の問題を克服せんとする気概が欲しいです。
踏むべき手順を踏めばそう難しくないということをこの解説で分かってもらいます。
まずは図に与えられた条件の数値や記号をガンガン書き込みます。
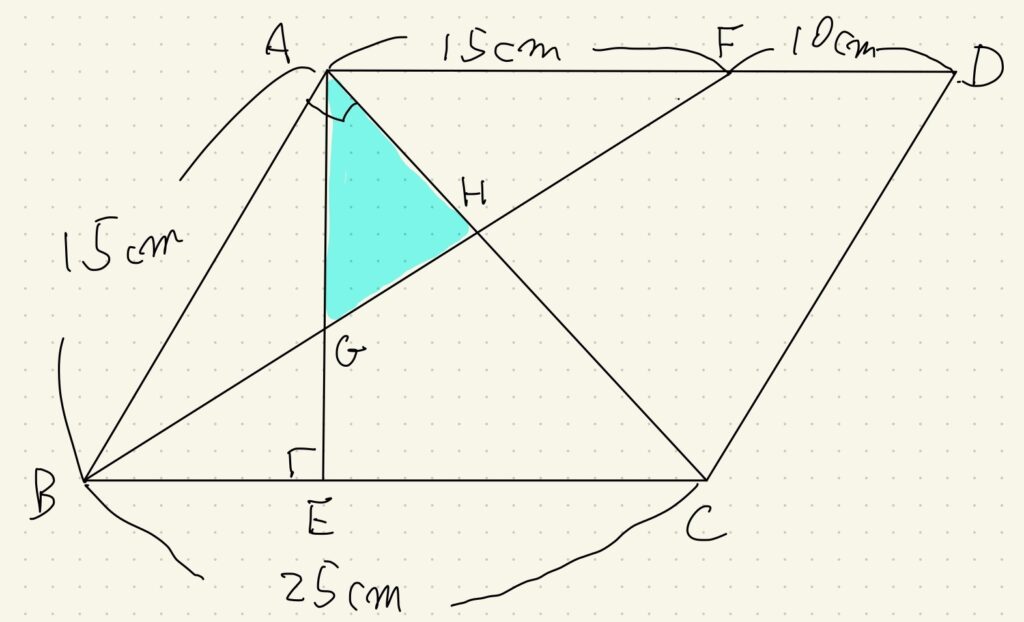
平行四辺形という条件があるので、「平行線がある→等しい錯角がある→相似が使える」と考えます。
錯角を利用した相似はリボンや蝶々の形になるのですぐに探せます。
三角形AHEと三角形CHBが相似で、相似比は\(15:25=3:5\)です。
直角条件から三角形ABCは三平方の定理で\(AC=20cm\)となり、面積が\(150cm^2\)と出せます。
これで、三角形AGHの面積はここを手掛かりと決めます。
ここで確認しておきたいのが、直角三角形の相似の頻出パターンです。
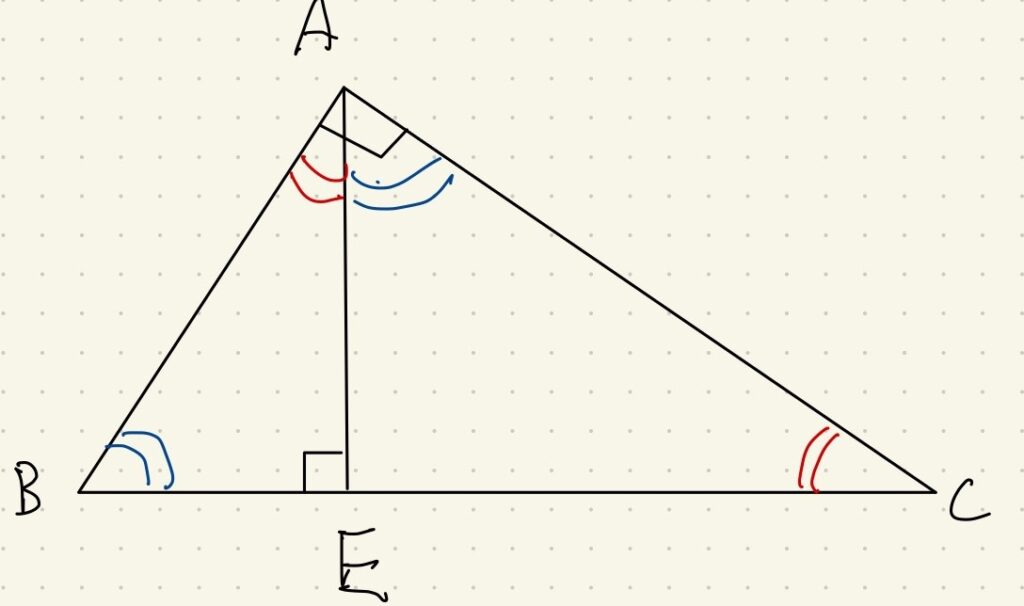
直角三角形の直角頂点から斜辺に垂線を下すと、上の図のように合同な角が現れます。
これは直角三角形の2つの鋭角和が90°になることを利用したものです。
上の図で言えば
\begin{eqnarray} \triangle ABC \text{∽} \triangle EAC \text{∽} \triangle EBA \end{eqnarray}これを使って辺\(BE=9cm\)が出せます。
そこでもう一度平行線の相似を取れば、三角形AGFと三角形BGFが相似で、相似比は\(15:9=5:3\)です。
ここで覚えておいて欲しい考え方が下の図です。
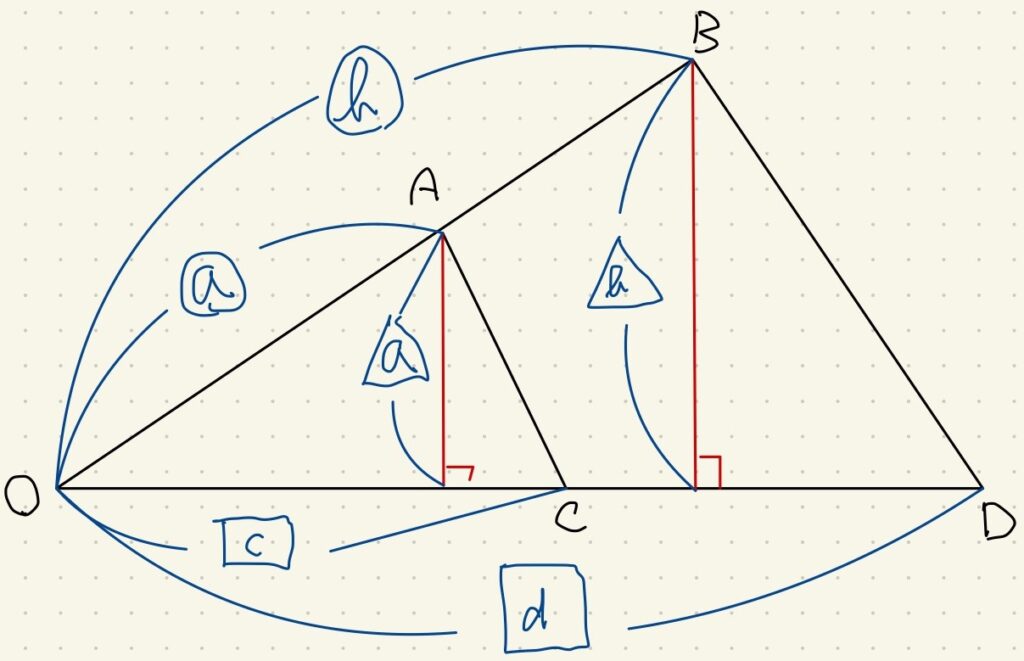
上の図で\(\triangle OAC と \triangle OBD \)は\(\angle A\)を共有している三角形です。
このとき辺\(OA:OB=a:b、OC:OD=c:d\)が分かれば、直角三角形の相似より\(\triangle OAC と \triangle OBD \)の高さ比も\(a:b\)であると分かります。
ということは\(\triangle OAC と \triangle OBD \)の面積比は\(\triangle OAC : \triangle OBD=ac:bd \)となります。
これを利用しましょう。
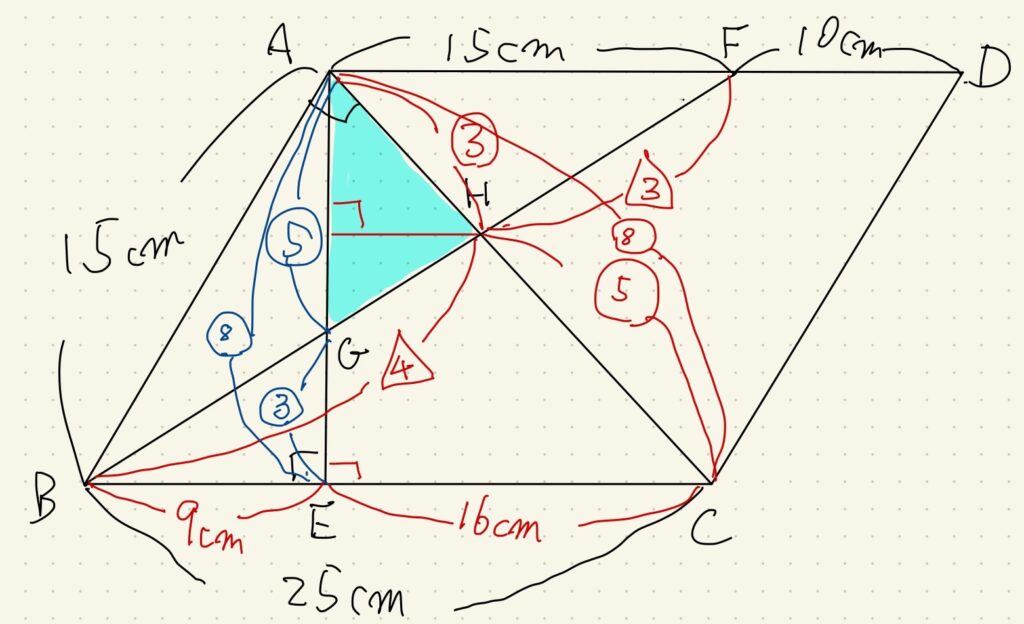

当初求めた\(\triangle ABC=150cm^2\)を使えば、底辺の比から\(\triangle AEC\)の面積が出ます。
そこから\(triangle AGH=s\)と置いて立式してみましょう。
\begin{eqnarray} \triangle AGH:\triangle AEC=3\times5:8\times8=s:150cm^2\times\frac{16}{25}\\ 15:64=s:96\\ s=\frac{15\times96}{56} s=\frac{45}{2}cm^2 \end{eqnarray}(エ)歯車の比の問題です。(20.8%)
ただの比例・反比例問題であるにも関わらずえらく正解率が下がりました。
これは過剰にパターンマッチングした学習のみに終始した生徒が多かったということです。
定期テストでも塾で配布した過去問に頼って点を取るような行動がありますが、それと同様です。
本質的な学力向上のための行動をとらず、目先の一問に小手先で対応する浅き学びモドキ、お先真っ暗まさに地獄とはこのことです。
閑話休題、歯車の基本に戻ります。
歯車Pが歯数pでa回転すると、それとかみ合う歯車Qが歯数qでb回転するとします。
動く歯の枚数は同じですから、\(ap=bq\)が成立します。
今回は歯車Pが歯数24で6回転/秒、歯車Qを歯数xでy回転/秒すると考えます。
これは\(24 \times 6=x \times y\)と表せます。
これより\(y=\frac{144}{x}\)ですので、歯車Qの歯数が36の時の回転数は\(y=\frac{144}[36}=4\)です。
問3の総評としては(ウ)以外は何があっても得点すべき領域だったと言えます。
あくまで日常から小手先の対応などせぬ汎用性の高い学習をしましょう。
問4
いつもの二次関数問題です。
最初に問題文を読んで、分かる点の座標をガンガン書いていきましょう。
点Aはx座標6ですから直線①\(y=x\)の式に代入して\(点A(6,6)\)です。
これを使ってy軸に対称な\(点B(-6,6)\)、点A・Bと同じy座標を持つ直線②\(y=-x+3\)上の\(点C(-3,6)\)を出します。
直線①と直線②の交点が点Dですから、\(点D(\frac{3}{2},\frac{3}{2})\)もすぐに出せます。
\(AO:OE=4:3\)という条件は点Aと点Eのx座標の絶対値も\(4:3\)だと言えます。
点Eはグラフよりx座標もy座標も負ですから、\(点E(-\frac{9}{2},-\frac{9}{2})\)となります。
直線②とx軸の交点ですから、y座標が0となり\(点F(3,0)\)、x座標が5なので、\(点G(5,-2)\)です。
ここまで記入を終えた後に、設問です。
(ア)点Aの座標を使って秒殺です。(89.0%)
\begin{eqnarray} y=ax^2 \\ A(6,6)を代入して \\ 6=36a \\ \frac{1}{6}=a \end{eqnarray}(イ)点Eと点Fの座標を使って秒殺です。(49.7%)
おなじみの連立方程式で関数式を出しても良いですが、以下の公式を証明できるようにして覚えておくと少し楽に解けます。
\begin{eqnarray} a≠cである2点(a,b)(c,d)を通る直線 \\ y-b=\frac{d-b}{c-a}(x-a) \end{eqnarray}繰り返しますが、証明できるようにしてから使うものです。
暗記して代入するだけなら連立方程式でやってください。
実際に使うと、下の様になります。
\begin{eqnarray} E(-\frac{9}{2},-\frac{9}{2})F(3,0)\\ y-0=\frac{0-(-\frac{9}{2})}{3-(-\frac{9}{2})}(x-3)\\ y=\frac{9}{6+9}(x-3)\\ y=\frac{3}{5}(x-3)\\ y=\frac{3}{5}x-\frac{9}{5} \end{eqnarray}あっという間に正解まで行けます。
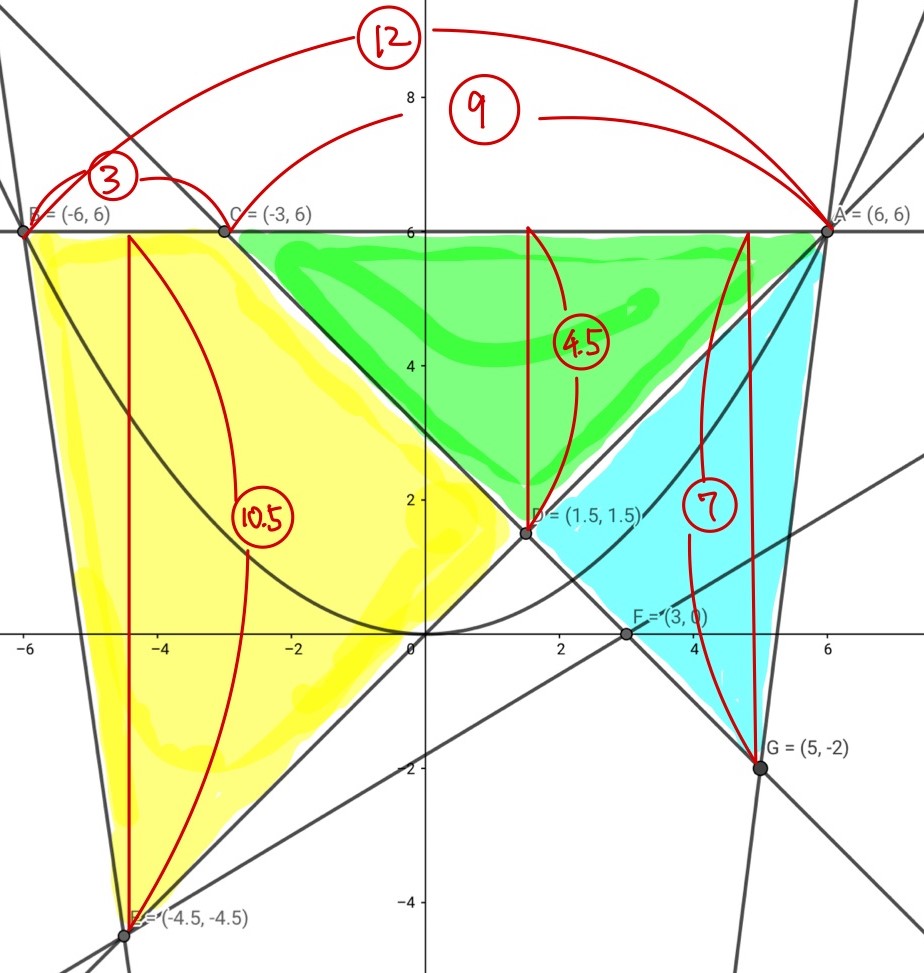
(ウ)神奈川名物・関数の面積比問題です。(3.9%)
偏差値55までの高校なら正解せずとも合格点になります。
正解率は例年低いので、苦手な人はノールックパスでも構いません。
しかし、理系大学進学を望むならこの程度の壁は乗り越えていきましょう。
三角形ADG と四角形BEDCの面積比を求めるものですが、後者が有名な図形ではありません。
一般に同じ大きさの角をもっている三角形は、その角をはさむ2辺の比で面積比が出せるというお話を先ほどしました。



これを考えると、以下の図のように見たくなります。
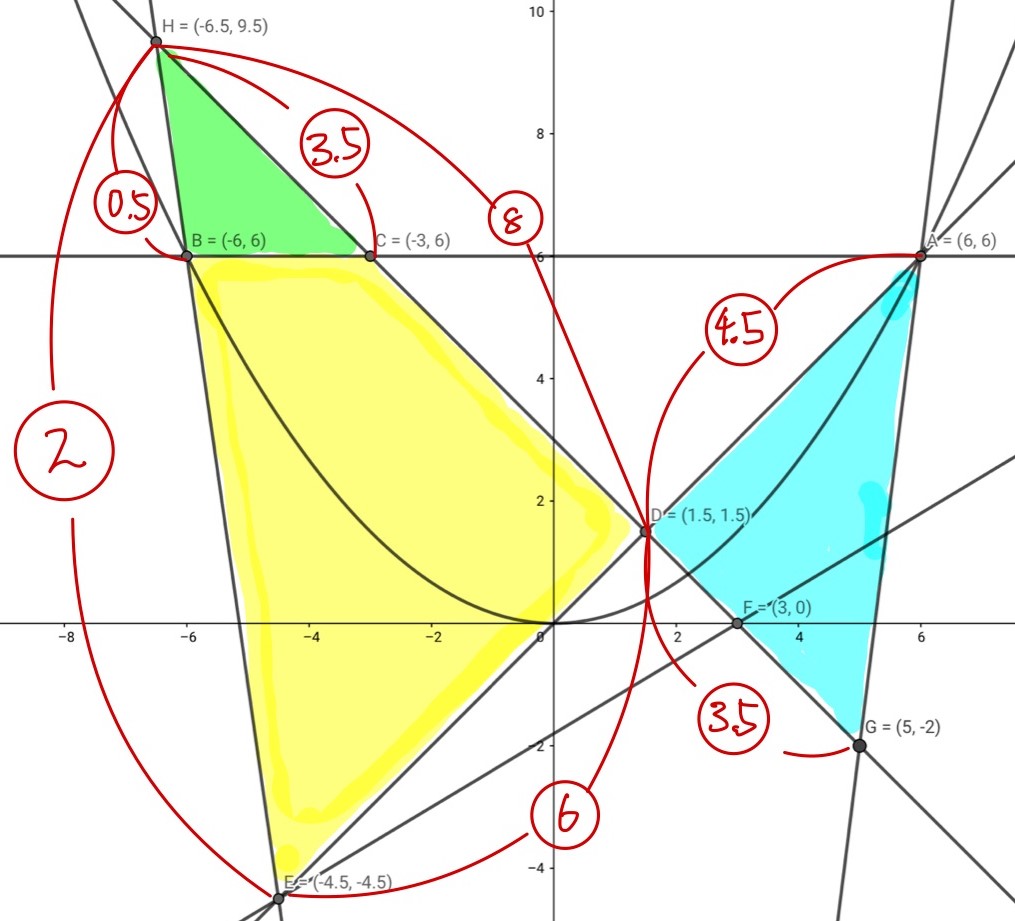

青と黄色は直接比較しにくいですが、青と黄+緑なら比較しやすいですね。
x座標同士・y座標同士で長さの比が出ますから、以下のように考えます。
\begin{eqnarray} 青:黄+緑&=&4.5\times 3.5:8\times 6\\ &=&9\times 7:16\times 12\\ &=&3\times 7:16\times 4\\ 黄:緑&=&8\times 2:3.5\times 0.5\\ &=&16\times 4:7\\ \end{eqnarray} \begin{array}{c|c|c|c} 青&黄+緑&黄&緑\\ \hline 3\times 7&16\times4&-&-\\ \hline -&16\times 4&(16\times 4-7)&7\\ \hline 21&64&57&7\\ \end{array} \begin{eqnarray} 青:黄=21:57=7:19 \end{eqnarray}三角形の底辺と高さの比から面積比を出すなら、以下のように考えるのもおすすめです。


問4の総評としては、(ウ)の計算量をどう素早く処理するかが、加点の差になる例年通りの出題でした。
問5
おなじみ確率の問題です。
神奈川県の県立高校入試の確率問題は「きっちり具体例を書け!さもなくば滅びよ!」です。
ということで今回もガチっと書いていきます。
まずは今回の事象について表にします。
\begin{eqnarray} \begin{array}{c|c|c|c|c|c|c} &B&C&D&E&F&G\\ \hline B&BH&BC&BD&BE&BF&BG\\ \hline C&CB&CH&CD&CE&CF&CG\\ \hline D&DB&DC&DH&DE&DF&DG\\ \hline E&EB&EC&ED&EH&EF&EG\\ \hline F&FB&FC&FD&FE&FH&FG\\ \hline G&GB&GC&GD&GE&GF&GH\\ \end{array} \end{eqnarray}ここに対象となるものをチェックしていきます。
私はこういう表を「\(6\times 6\)表(ろくろくひょう)」と呼びます。
入試本番でも、必ず表にして書きましょう。
(ア)確率の基本問題です。(66.8%)
この問題について言えば題意を満たすのは「点の候補としてとれるBCDから異なる2点を選ぶ」ことになります。
このぐらいであれば表の力を借りずとも解けます。
\begin{eqnarray} \begin{array}{c|c|c|c|c|c|c} &B&C&D&E&F&G\\ \hline B&BH&\color{red}{BC}&\color{red}{BD}&BE&BF&BG\\ \hline C&\color{red}{CB}&CH&\color{red}{CD}&CE&CF&CG\\ \hline D&\color{red}{DB}&\color{red}{DC}&DH&DE&DF&DG\\ \hline E&EB&EC&ED&EH&EF&EG\\ \hline F&FB&FC&FD&FE&FH&FG\\ \hline G&GB&GC&GD&GE&GF&GH\\ \end{array} \end{eqnarray}これで、\(\frac{6}{36}=\frac{1}{6}\)
(イ)確率の標準問題です。(12.3%)
こちらの問題は、対象となる立体の観察から始めます。
今回は立方体が相手なので、1辺の長さを1とおくと立方体上の2点を結ぶ線分の長さは以下の三通りです。
- 条件①;立方体の1辺=1(以後①)
- 条件②;ある面の対角線=\(\sqrt 2\)(以後②)
- 条件③;立方体内部の対角線=\(\sqrt 3\)(以後③)
Aと決まった2点で出来る3つの辺の長さがすべて異なるということは、上の条件を満たす位置の組み合わせを探すということです。
Aから各点への距離は以下の通りです。
\begin{array}{c|c|c|c|c|c|c} &B&C&D&E&F&G\\ \hline A&AB=1&AC=\sqrt 2&AD=1&AE=1&AF=\sqrt 2&AG=\sqrt 3 \end{array}他の2点の距離は以下の通りです。
\begin{eqnarray} \begin{array}{c|c|c|c|c|c|c} &B&C&D&E&F&G\\ \hline B&BH=\sqrt 3&BC=1&BD=\sqrt 2&BE=\sqrt 2&BF=1&BG=\sqrt 2\\ \hline C&CB=1&CH=\sqrt 2&CD=1&CE=\sqrt 3&CF=\sqrt 2&CG=1\\ \hline D&DB=\sqrt 2&DC=1&DH=1&DE=\sqrt 2&DF=\sqrt 3&DG=\sqrt 2\\ \hline E&EB=\sqrt 2&EC=\sqrt 3&ED=\sqrt 2&EH=1&EF=1&EG=\sqrt 2\\ \hline F&FB=1&FC=\sqrt 2&FD=\sqrt 3&FE=1&FH=\sqrt 2&FG=1\\ \hline G&GB=\sqrt 2&GC=1&GD=\sqrt 2&GE=\sqrt 2&GF=1&GH=1\\ \end{array} \end{eqnarray}今回は数値を書き込みましたが、入試本番では①に〇・②に△・③は無印ぐらいで見分けられれば問題ないです。
該当する組み合わせを確認してカウントしましょう。
合計16通りありますので、確率は\(\frac{16}{36}=\frac{2}{9}\)となります。
問5の総評としては、確率の問題は数え上げの速さ・正確さがカギだということです。
数学が苦手な人ほど、確率の数え上げは練習しておきましょう。
問6
(ア)立体の表面積を求める問題です。(50.6%)
一辺が分かっている正三角形の面積さえわかればよいのですが、これが半数しか出来ていないのはいただけません。
どれだけ学習をしない受験生が神奈川県にいるのかと思います。
正三角形にせよ二等辺三角形にせよ、頂点から底辺に向かって垂線を下して二等分線とすれば、合同な直角三角形が2枚できます。
そうすれば三平方の定理で高さが出せるので、面積も分かります。
正三角形の面積公式として暗記する人もいますが、理屈を理解しておけば覚えるまでもないです。
\begin{eqnarray} 1辺6cmの正三角形の高さhについて\\ h^2&=&6^2-3^2\\ h&=&3\sqrt 3\\ 正三角形の面積&=&6\times 3\sqrt 3 \times \frac{1}{2}\\ &=&9\sqrt 3\\ 正方形の面積&=&6^2\\ &=&36\\ よって36+9\sqrt 3cm^2\\ \end{eqnarray}(イ)立体の体積を求める問題です。(34.6%)
立体の体積は底面積と高さが分かれば計算できます。
底面積と高さは必ず垂直になる性質があります。
今回は展開図に2枚の直角三角形がみえるので、これをヒントにします。
組み立てる際に\(\triangle ADE\)を底面として高さ\(BE\)を使えば体積が分かります。
先ほどの(ア)で\(\triangle ADE\)の面積が出ているので、以下の通りです。
\[底面積\times 高さ\times \frac{1}{3}=9\sqrt 3\times 3\times \frac{1}{3}=9\sqrt 3cm^2\](ウ)線分の長さを求める問題です。(0.5%)
圧倒的に正解率が低かった問題です。
立体図形の最後の問題にはたまにあることですが、ほぼ合否には影響しません。
大半の受験生が「合格点」を取るためなら、いったんパスして他の問題をガッチリとるのが上策です。
その上で高校以降で理系難関大学進学を目指す志のある生徒諸君はチャレンジです。
最短距離を求める問題の基本は「点から線(または面)へ垂線を下した長さ」です。
今回は立体の表面上に引かれた線分が対象ですので、展開図で考えます。
問題で示された展開図では、求める線分が分割されて引かれるので考えにくいです。
そこで、展開図を切り離して組みなおして見やすくします。
書きなおした展開図はこちらです。
このままでは謎の五角形を見つめることになるので、補助線を引いて知っている形にします。
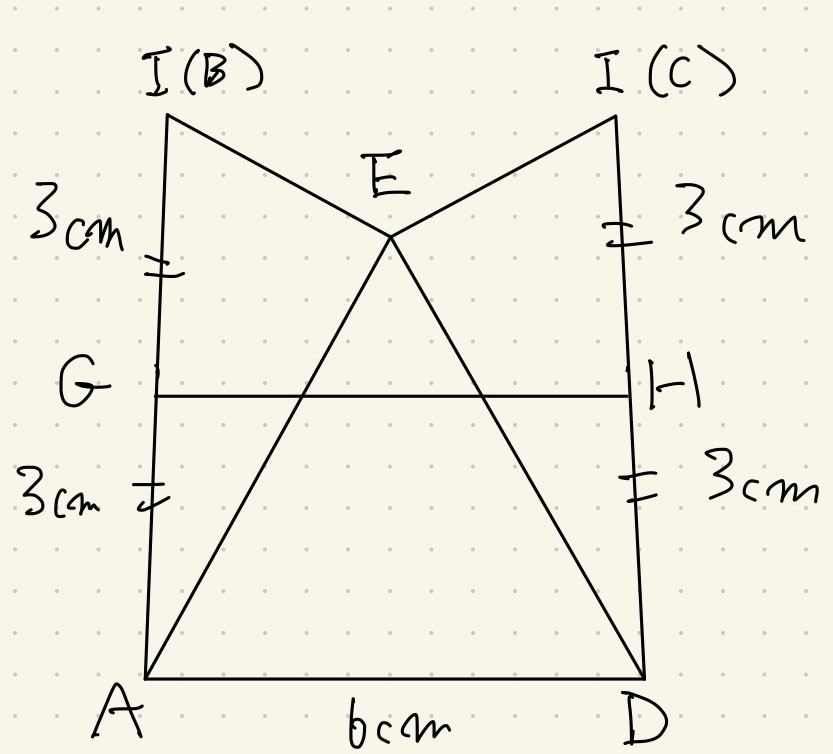

正三角形の左右に合同な直角三角形を張り付けていますから、図形が左右対称に見えます、
左右対称な図形の代表例が等脚台形です。
補助線によってこのような図形になります。
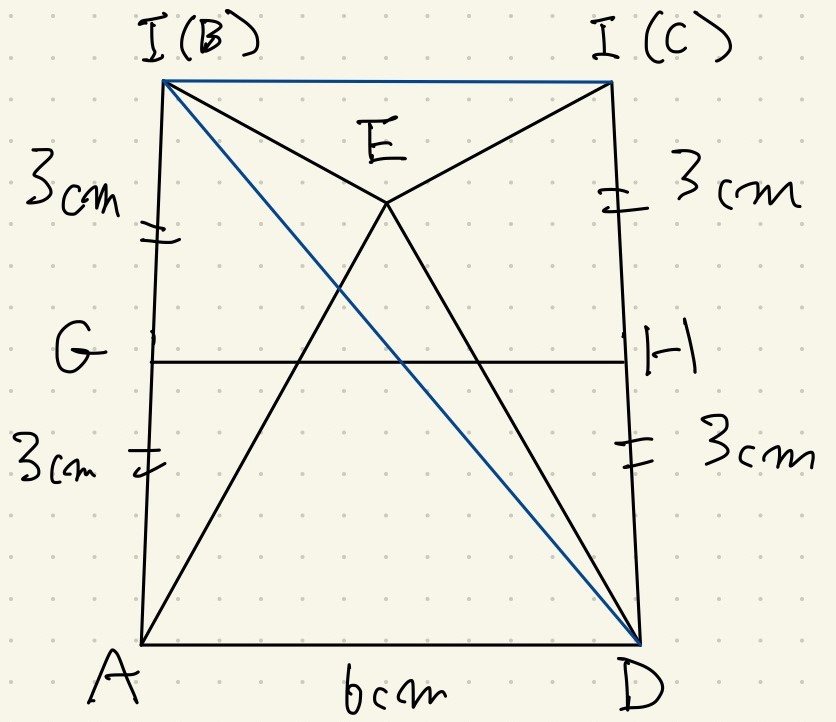

台形は対角線を引くと扱いやすくなります。
求めるGHはこの台形での中点連結部分になります。
GHの左側は三角形IADの中点連結定理が使えるので、すぐに3cmだと出ます。
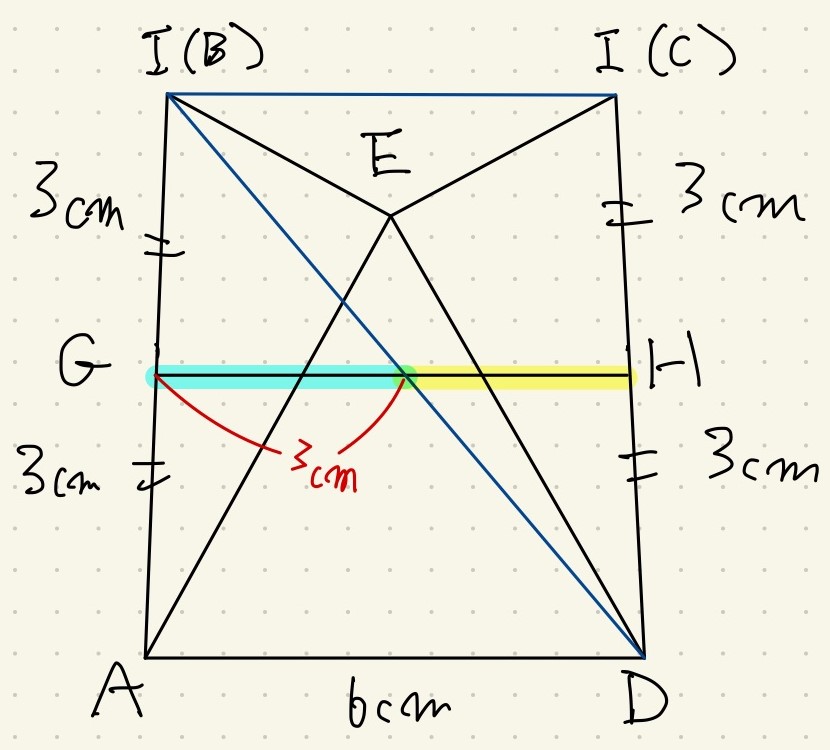

残る右側の黄色い部分ですが、これも三角形I(B)DI(C)の中点連結定理で分かりそうです。
ここで台形上底のI(B)I(C)を出すために、補助線を引きます。
左右対称な図形は二等分するという意識を忘れずに。
ここで図形をよく観察すると、中央の部分にこのような角度を発見できます。
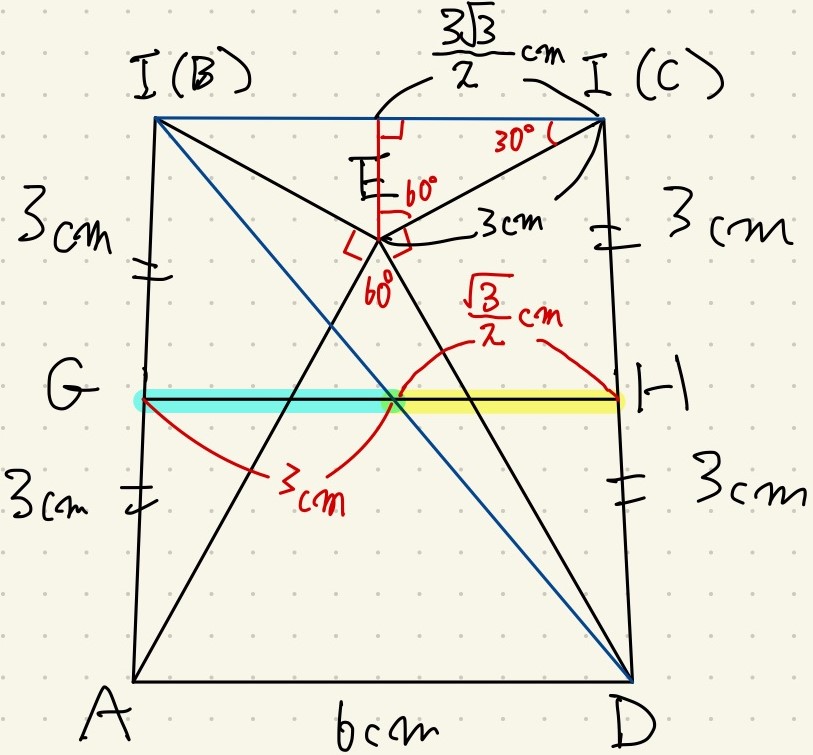

\(360^{\circ}-60^{\circ}-90^{\circ}\times 2=60^{\circ}\times 2\)
ということは、出来た直角三角形は\(30^{\circ}・60^{\circ}・90^{\circ}\)の直角三角形です。
ということで、三平方の定理で長さを求めることが出来ました。
中点連結定理があるので、このようになります。


よって、\(GH=(3+\frac{3\sqrt 3}{2})cm\)です。
全体講評
2020年は問3(ウ)問4(ウ)問6(ウ)が特に難しい一問でした。
この3問を失点しても県立相模原までなら対応は可能です。
ただし、裏を返せば他の問題をいかに確実に倒すかということです。
難問であれば即撤退してまず取れる問題を確保して、難問三つから余分に得点するような判断が重要です。
標準問題にいかに素早く対応できる正確な計算力を身に着けておくかを念頭に置いて、学習していきましょう。
名門公立高校が君を待っています。