2022年　神奈川県公立高校入試　数学　解説

今日は神奈川県の公立高校入試の学力検査が実施されました。

今日はまず、2022年度の数学の問題について検討してみましょう。

問題をお持ちでない方は以下のリンクからでも入手できます。

問1

(ア)普通に正負の数の加減問題でした。特に問題ないでしょう。

(イ)同じく分数の正負の数の加減問題でした。通分さえ間違えなければ良いです。

(ウ)同じく通分を意識する問題ですが、符号の分配に注意しましょう。

おすすめは全体を最小公倍数の12という分母で書いて計算するやり方です。

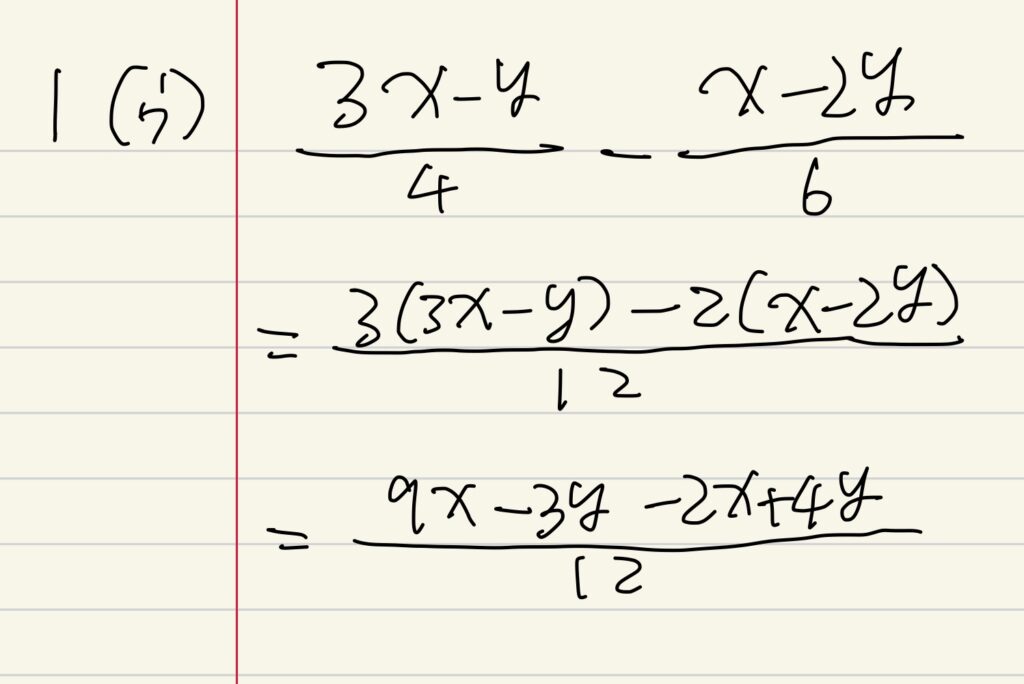
模範解答もこちらで書いてありますしね。

(エ)神奈川県の入試では毎度出される平方根加減です。

分母に出てくる平方根に注目すれば、もう一つの平方根をどの様に扱うかのヒントになります。

今回は√32＝√16×√2と＝4√2とできますね。

分母の平方根を取り外した残りが、平方数になっていることを確認してください。

そうなっていない場合には計算ミスです。

(オ)二次式の計算問題です。大体二次式同士の減法で出題されますが、これは符号ミスを誘うためです。

符号の分配ミスがないように途中式を書く癖がついている生徒にはどうということはないです。

問1の総評としては、ここまでは平穏無事だと言えます。

例年通りの準備ができていればそのまま得点できたでしょう。

ここでは時間を食わないことが何よりです。

問2

(ア)小数分数の係数を持った連立方程式もお馴染みのものです。

特に問題なく得点できたことと思います。

(イ)同じく例年通りの二次方程式の解を求める問題です。

今年の問題であれば解の公式を利用してお終いです。

√33に一瞬ギョッとしますが、そもそも選択肢もそれしかないので、符号ミスさえ無ければ良しです。

(ウ)二次関数の値域問題です。

この問題を取るために必ずグラフを書く癖をつけましょう。

二次の係数が負なので、上に凸のグラフを描いて変域を書き込めば、間違う可能性を減らせたはずです。

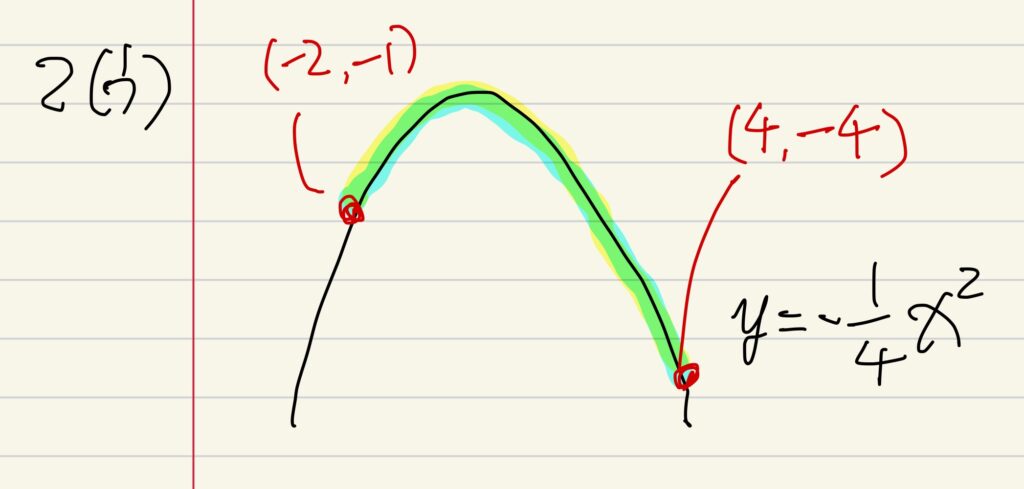
このように定義域を意識して色までつけておけば、最大値が0であることも見落としません。

舐めてグラフを描かなかったりポイントの数字や範囲を目立たせずに失点するのは論外です。

(エ)一次方程式の文章題です。

求めるA班の人数をaとおいて式を立てればお終いです。

方程式は等式ですから、「何について等しい話にするか」を意識しましょう。

今回の問題であれば椅子の数について比較しているので、椅子の数についての等式を書きましょう。

問題文を読んで何について式を書くかを意識する練習は、遅くとも中1には手をつけなくてはいけません。

(オ)平方根の混じった式の値を求める問題です。

単純に代入して終わり、でも解けなくはありませんが計算量が増えます。

代入前に因数分解をしておくと楽になる問題があるので、一度は試しましょう。

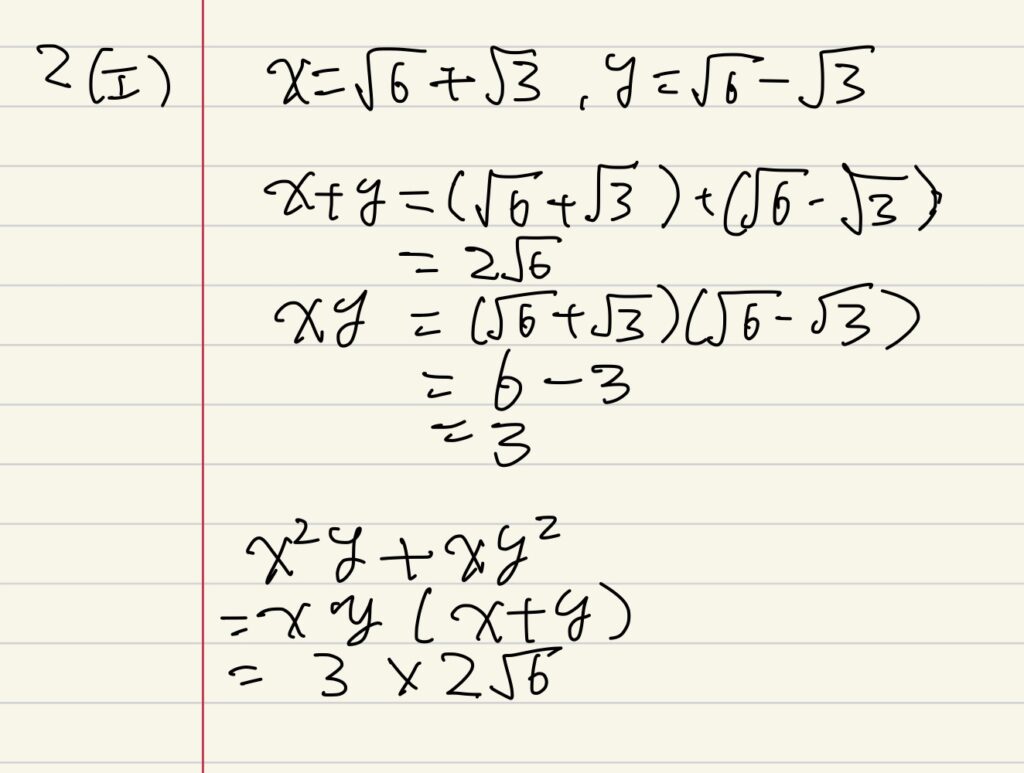
問2の総評としては、これもほぼ例年通りの難度であったと考えます。

ここまでは順調にきた受験生も多いでしょう。

問3

(ア)(i)合同証明問題です。

相似証明ではなくて簡単かと思いきや、例年より条件文が多く時間を取られた生徒も多いでしょう。

難度としてはあまり大したことはありませんので、合同証明を練習してさえいれば中2でも解けます。

(ii)角度の問題です。

(i)の問題を証明する際にどこの角度が等しいかを確認できていれば正解はわりに簡単に出ます。

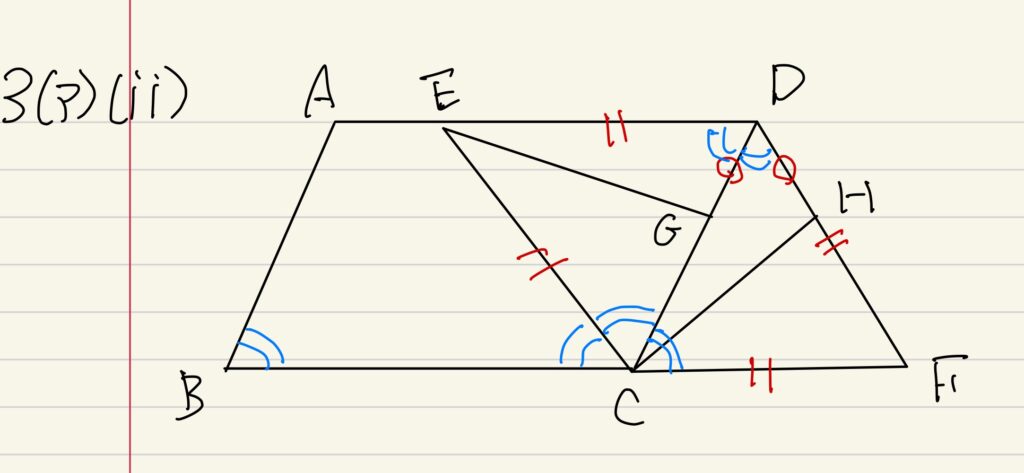
(i)で出た条件に「四角形CFDEが平行四辺形」という条件を併せると、四角形CFDEがひし形になります。

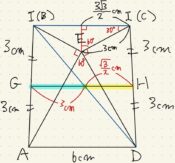
ひし形は対角線で内角を二等分できますから、上図のように∠BCE＝∠ECD＝∠DCF＝60°です。

(イ)統計問題ですが、ここが確認事項が多くて時間をかなりくいます。

完全に後回しにすべき問題だったと言えます。

説明5より、「2年生と3年生の最頻値は等しい」ので、選択肢「1、2、3、4、6」だけ相手にします。

説明1より、1年生の中央値の階級「22-26」と同じ選択肢「1、2」が2年生として残ります。

説明2より、30回以上の生徒の割合は1年生が7/38、選択肢1で4/40、選択肢2で9/40を確認します。

「2年生の方が小さい」と言われますので、選択肢1と2で小さい1を選びます。

馬鹿正直に7/38と大小比較する前に確認すべきですよね。

説明3より、1年生の最大値は階級「34-38」にあるので選択肢「4、6」が3年生として残ります。

説明4より、14回未満の生徒の割合は1年生が4/38、選択肢4で6/40、選択肢6で4/40を確認します。

「3年生の方が小さい」と言われますので、選択肢4と6で小さい6を選びます。

馬鹿正直に4/38と大小比較する前に確認すべきですよね。（リピート）

こういう行動が地味に時間を短縮します。

何を問われているかを全力で考えてください。

(ウ)円周角を用いた角度問題です。

ポイントはBCに線を引くことで現れる左右対称な等脚台形です。

円に内接する四角形は対角の和が180°、そして等脚台形は上底と下底の二角がそれぞれ等しくなります。

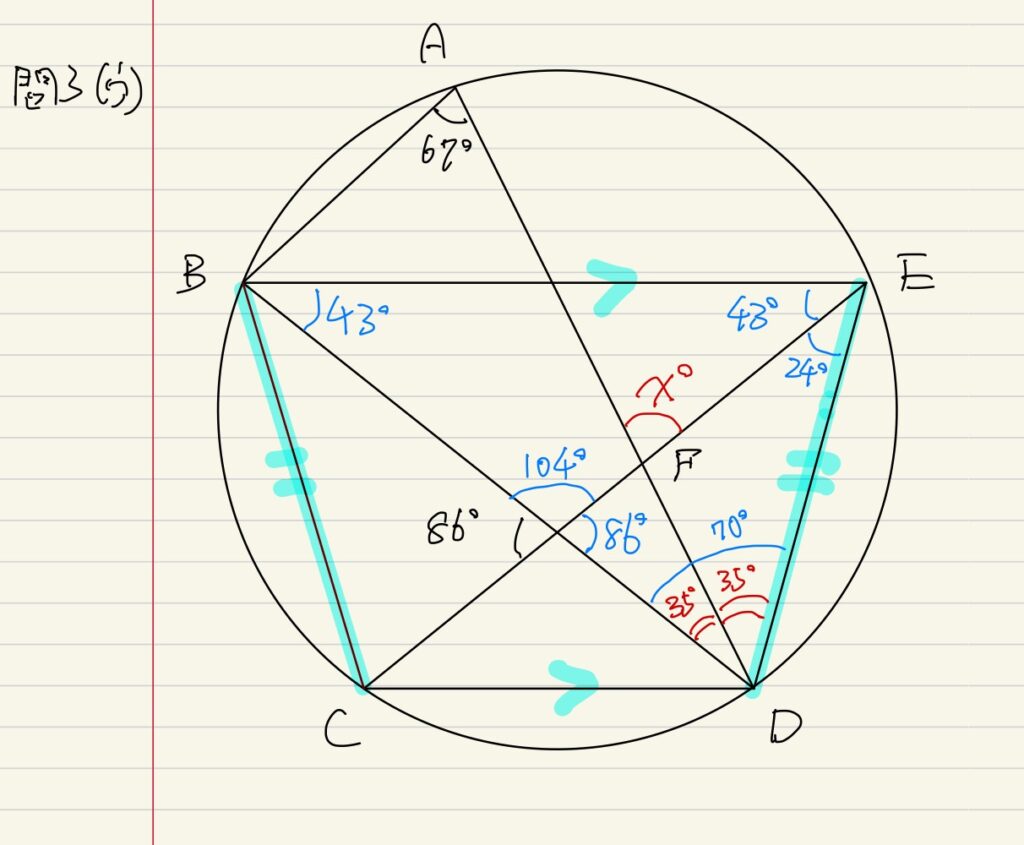
∠AFEを求めるには三角形の内角和を用いるか、対頂角CFDが分かれば良いはずです。

今回は後者を考えます。

理由は「ADが∠BDEの二等分線」という条件が使いやすそうだからです。

まず中央の86°から対頂角86°と外角104°を決定します。

等脚台形は対角線で現れる底角の一部を使った三角形も左右対称になるので、二等辺三角形が見えますね。

この底角43°が分かれば、円周角67°を参考にして∠BDE70°まで分かります。

ここで最初に検討を付けた「ADが∠BDEの二等分線」という条件から∠BDF30°が分かって終了です。

常に方針を立てて解けば比較的少ない試行錯誤で解けます。

そしてその方針は、常に問題文をヒントにしましょう。

(エ)三角形の面積を求める問題です。

これも苦手な人はパスして後ほど、で良かったでしょう。

条件から解法を検討していきます。

直径が含まれる図形問題は円周角の定理から直角三角形を探すのが基本です。

色を付けた部分の面積を求める問題ですが、直角三角形ABDの一部であることが分かります。

直角三角形は面積を求めやすいので、そこを取っ掛かりにしてみます。

欲しいのはADとBDの長さです。

与条件より∠ACB＝∠AED＝90°です。

AEとEDの長さが分かっていますから、三平方の定理でAD＝√13cmが出せます。

ということはBDが分かれば三角形ABDは出せます。

ここでAEとECの長さが分かっていますからこれを使えないかと考えます。

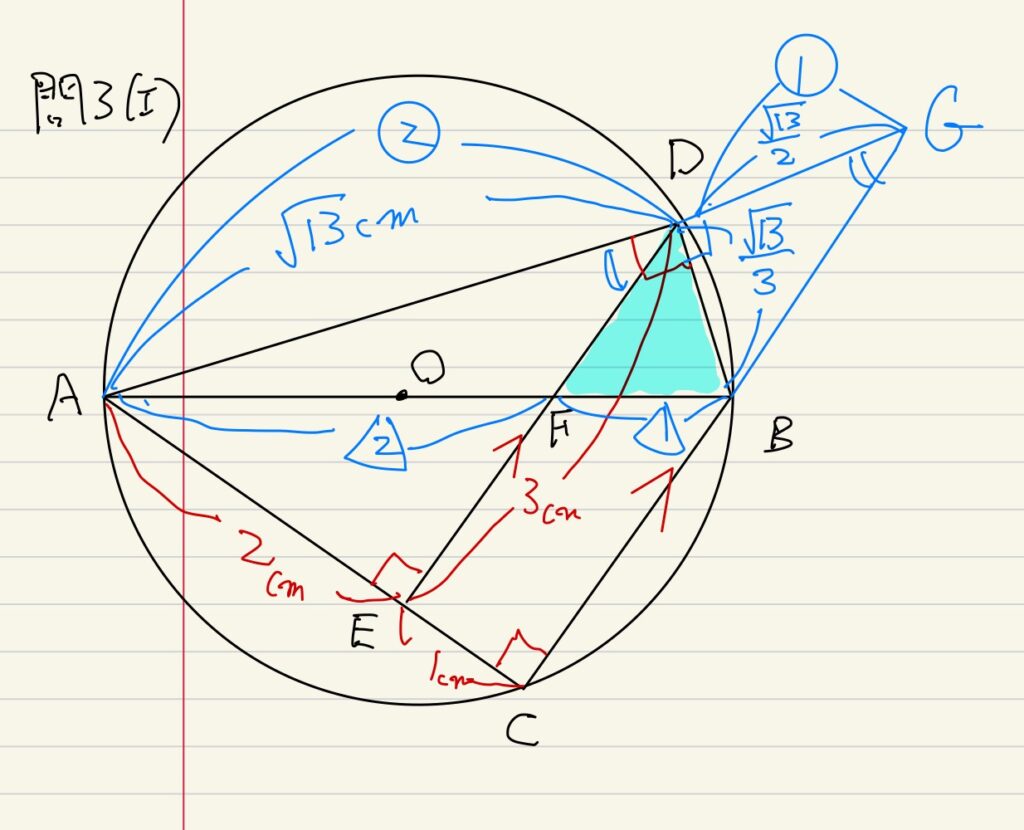
ここで同様に三角形AEDと相似な三角形があるといいと考えて、円の外にADとCBを伸ばします。

これで出来た三角形ACGと三角形AEDが相似ですから、AD:DG=2:1も言えました。

これを使ってDG=√13/2cmが導けました。

ここで∠ADB =∠GDB=90°かつ平行線の同位角を考えると、三角形AEDと三角形BDGも相似であると言えます。

よってAE:ED=BD:DG=2:3を用いてBD=√13/3cmが分かりました。

これで直角三角形ABDの面積が13/6㎠となります。

三角形ACBと三角形AEFの相似が分かりますから、AE:EC=AF:FB=2:1を使えばゴールです。

高さの等しい三角形は底辺比が面積比になりますので、正解が分かります。

恐らく答案中盤の、円の外へ延長する補助線が引けない生徒が多かったでしょう。

＜追記＞

上記の答案は、私が初回に50分制限の中で作った答案です。

しかし帰宅して布団の中で別解を考えた時に、別の視点の解説をできると気づいたので書きそえます。

課題になった直角三角形の面積を、円の中だけで考えてみます。

直角三角形の鋭角DABが円周角ですから、これと孤が同じ円周角を探しました。

既存の線では作れなかったので、青い補助線CDを引いてみます。

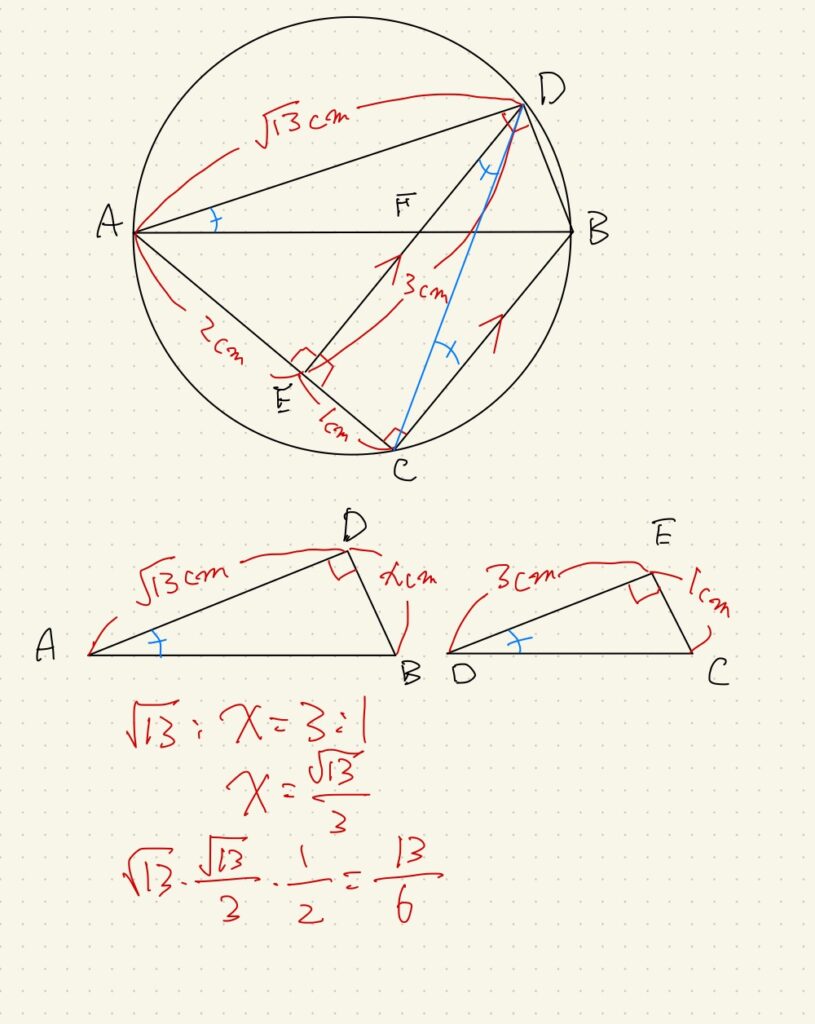
これで出来た三角形CBDは直角三角形ではありません。

しかしBC//DEという条件を使えば、錯角で直角三角形CDEを見つけられます。

鋭角と直角がそれぞれ等しいので、三角形ABDと三角形DCEが相似であると言えます。

相似比を使って、赤字の計算式で直角三角形の面積まで辿り着けます。

以降は上記答案と同様に行けます。

問3の総評としては「飛ばすものは飛ばす勇気」が無いとここでタイムロスをしたり心を折られて残りが鈍くなってしまったのではないかと考えます。

問4

いつもの二次関数問題です。

最初に問題文を読んで、分かる点の座標をガンガン書いていきましょう。

点Aはx座標6ですから直線①の式に代入してA(6,9)です。

これを使ってy軸に対称なB(-6,9)、Bと同じx座標のC(-6,-3)、D(-6,0)を決めます。

DO:OE=6:5よりE(5,0)を(6,0)と勘違いしては地獄です。

ここまで記入を終えた後に、設問です。

(ア)点Aの座標を使って秒殺です。

(イ)点Cと点Eの座標を使って秒殺です。

おなじみの連立方程式で関数式を出しても良いですが、以下の公式を証明できるようにして覚えておくと少し楽に解けます。

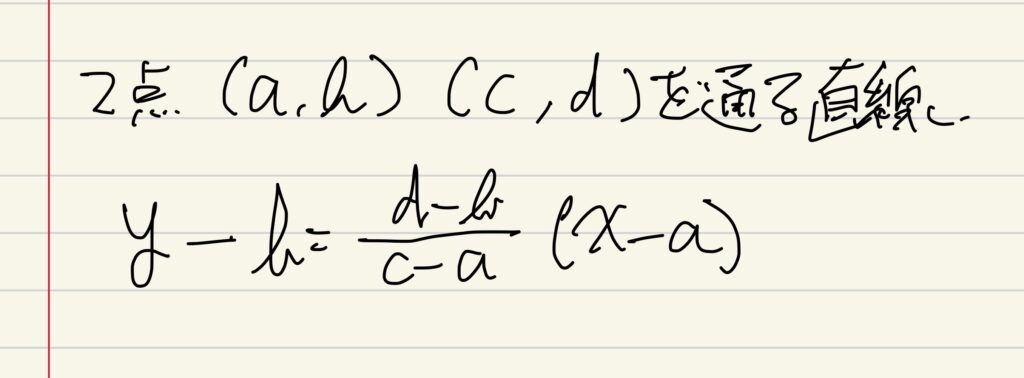
繰り返しますが、証明できるようにしてから使うものです。

暗記して代入するだけなら連立方程式でやってください。

実際に使うと、下の様になります。

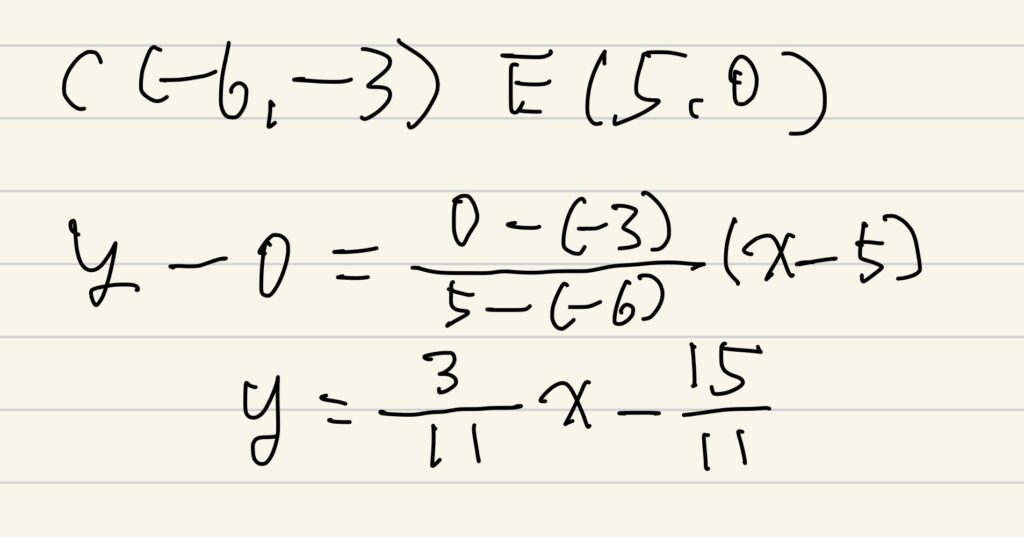
あっという間に正解まで行けます。

(ウ)神奈川名物・関数の面積比問題です。

偏差値55までの高校なら正解せずとも合格点になります。

60以上の高校を目指すなら、なんとか追いつきたいレベルです。

ここで苦戦した人もいるかと思いますが、問題文をきちんと読むとそこまで大した計算がなく解けます。

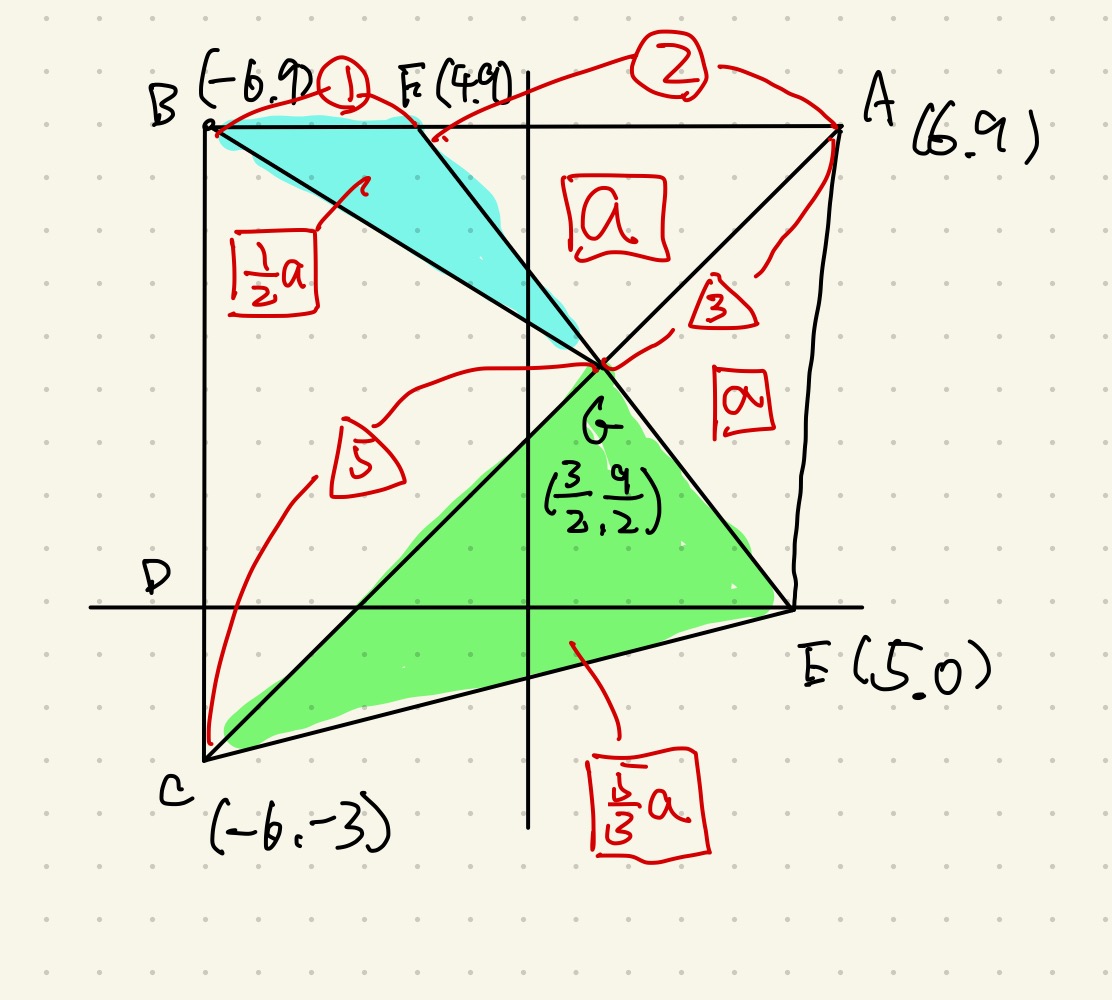
まず、三角形AFG＝三角形AEGとなるように点Fと点Gが設定されていることが分かります。

ということは、それぞれの底辺はFG=EGとなります。

Eのy座標が0、Fのy座標が9ですからGのy座標は9/2です。

ということはGのx座標が3/2ですから、Eのx座標5からFのx座標−2が出ます。

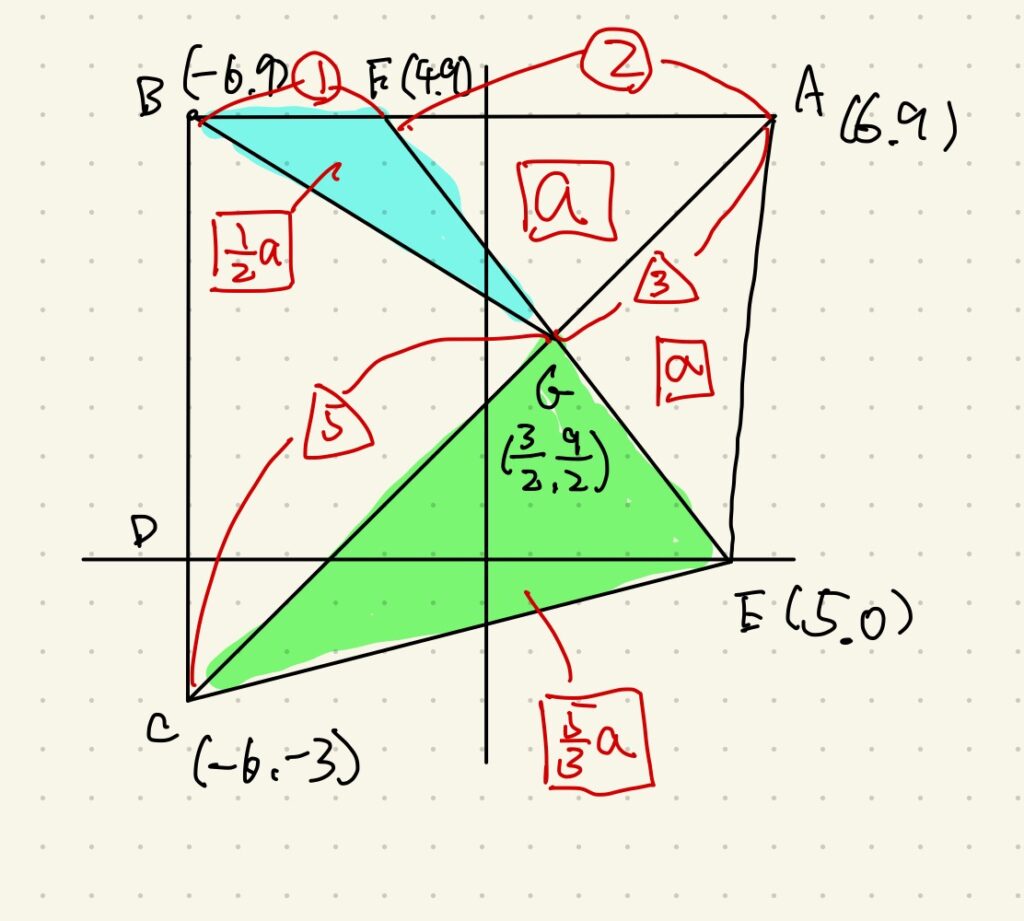
分かった座標を書き込んでみると、上の図が書けるはずです。

青と緑の三角形の比を求める問題ですから、基準となる等しい面積の三角形AFGと三角形AEGの面積を□aとおいて考えます。

青も緑も「高さの等しい三角形の面積比は底辺比に等しい」という性質を使えば□a/2、□5a/3と表せます。

この二つの比を簡単にすれば正解まで辿り着きます。

他にも平行四辺形を探せるとGの座標を考えずにFの座標を出して解くという解法もあります。

問4の総評としては、(ウ)の計算量が多いところをどれだけ素早くできるかが鍵であったと言えます。

問5

おなじみ確率の問題です。

神奈川県の県立高校入試の確率問題は「きっちり具体例を書け！さもなくば滅びよ！」です。

ということで今回もガチっと書いていきます。

(ア)正方形の面積が等しくなるわけですから、PR=RQであれば良しです。

つまりa=bだけですから、(a,b)=(1,1)(2,2)(3,3)(4,4)(5,5)(6,6)で6通りです。

確率は6/36=1/6で秒殺です。

(イ)Xの面積がYの面積より25㎠以上大きいという条件です。

ここでこの条件を式にしてみます。

PR=xcm、RQ＝10-xcmとして25㎠差がついたとすると、以下の式になります。

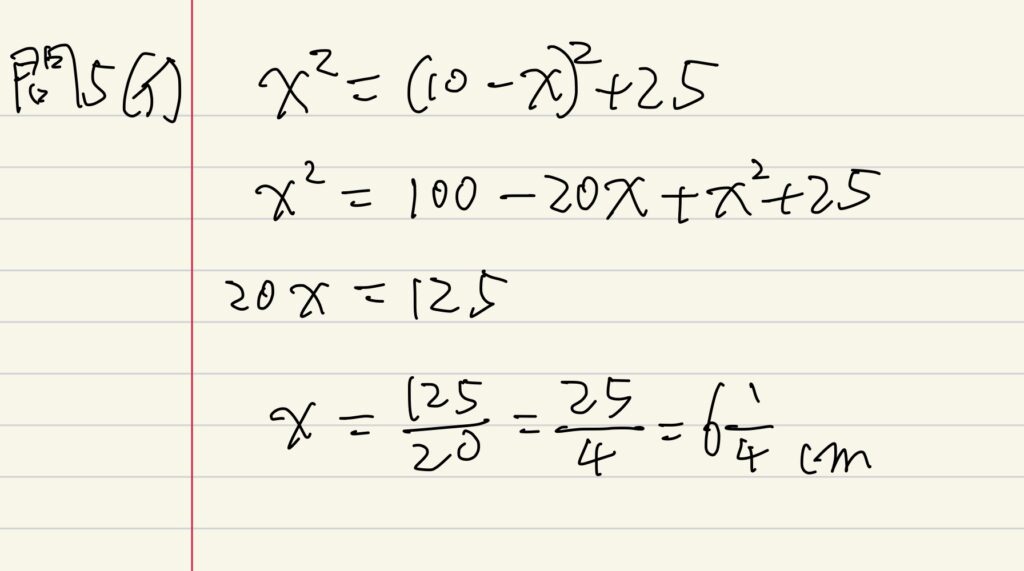
これで、PRが最低でもどれだけの辺の長さがあればいいかが分かりました。

これより長くなれば条件を満たしますので、それを探しに行きます。

以下のように表を埋めていきます。

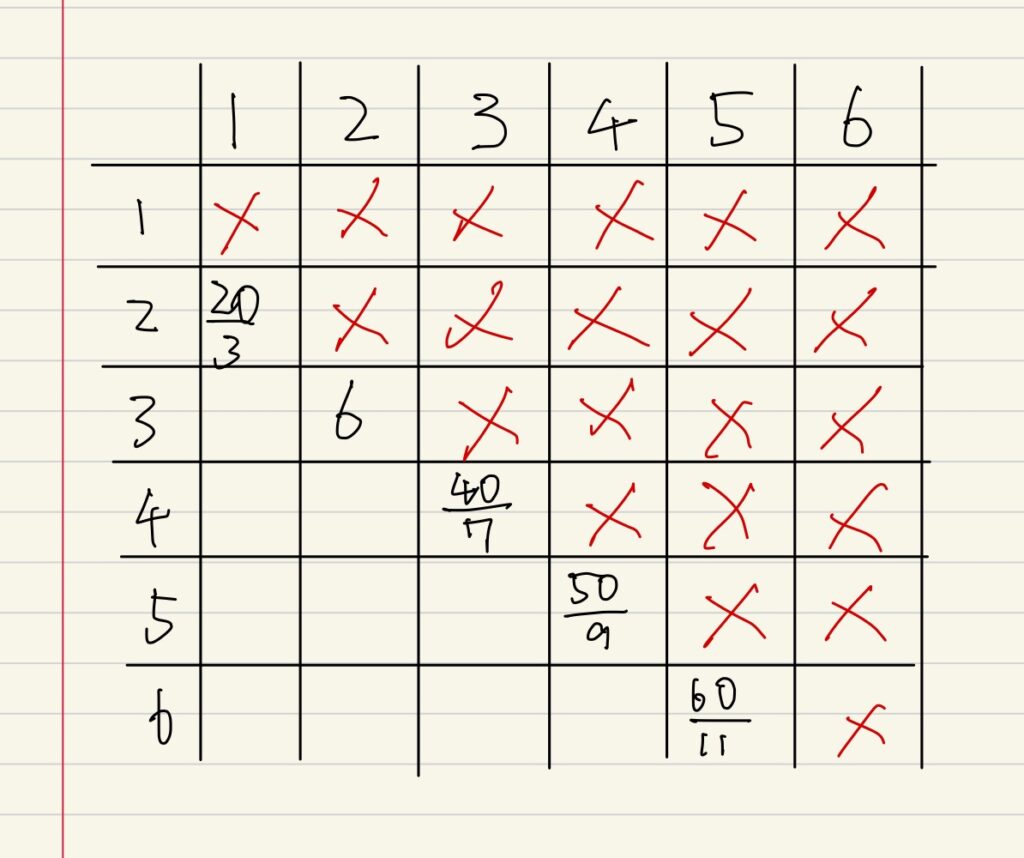
表の左端がaの値、上端がbの値です。

PRの方が長くなるのでa>bとなる部分以外は絶対にアウトですから除外して×をつけました。

その境目のなる5パターンだけ、PRの長さを計算して出しました。

これらの中で先ほどの25/4より大きいものだけチェックすると以下のようになります。

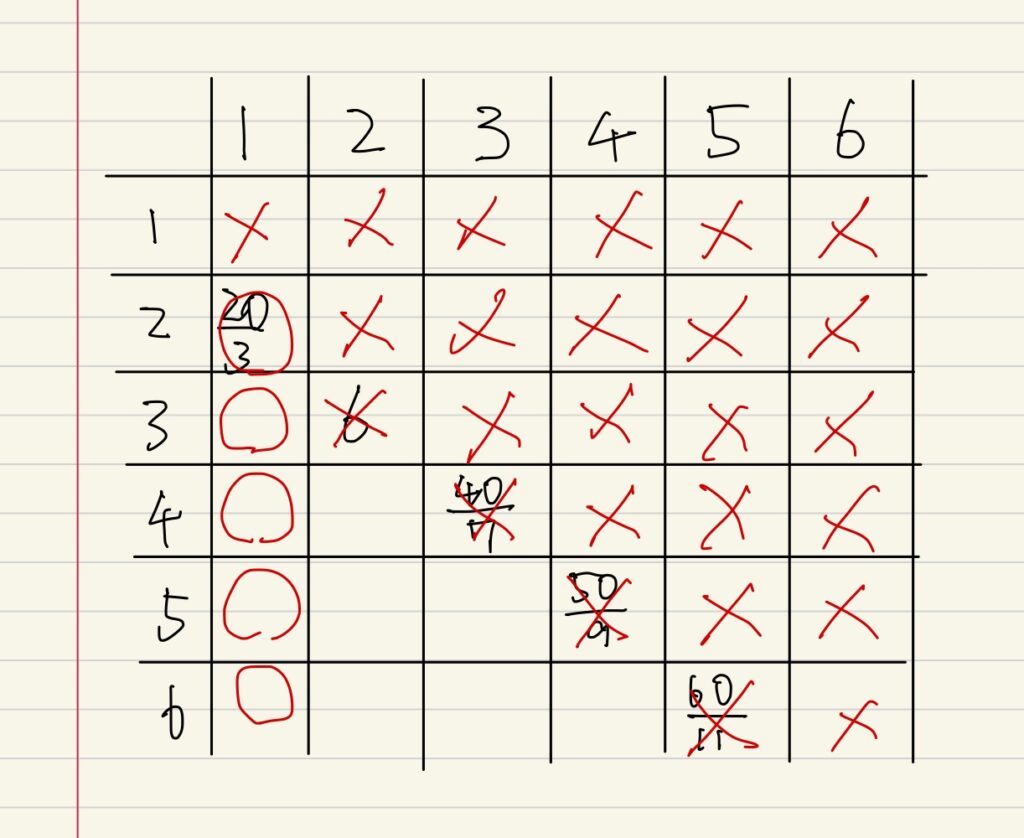
〇がついたものより下にいけばPRが長くなるだけですから、条件を満たすので続けて〇をつけてよいです。

条件を満たさなかったものは×をつけて、さらに一段下の値を書いて同様に確認していきます。

そうすると以下のようになります。

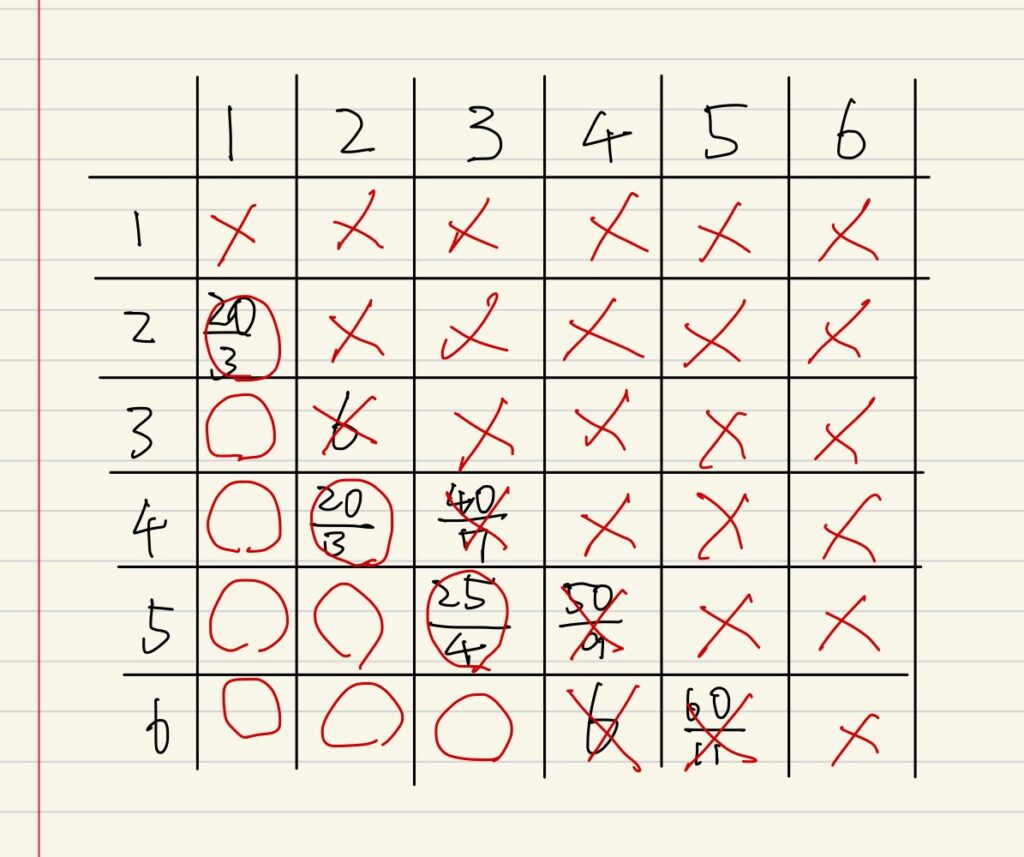
これで〇がついたものの数を数えれば10通りであることが分かります。

よって求める確率は10/36=5/18です。

問5の総評としては、やはり神奈川県の公立高校入試数学において確率は優先してとくべき問題であったということです。

特に今年のように面倒な問題を含んでいればなおさらでしょう。

問6

(ア)立体図形の体積問題です。

以下のように台形が底面ですから、高さを求めるために補助線を引いてみます。

というより、問題文中に斜めにひかれた5cmがあれば「3:4:5」という直角三角形を探してみて欲しいですね。

あっという間に三平方の定理で台形の高さが4cmであると分かるので、底面積を求めて体積にして秒殺です。

(イ)三角形BDGの面積を求める問題です。

こういう問題を解くときには絶対に・何が有ろうと・親を人質に取られても与えられた図以外に三角形の書き抜きをしてください。

BDとGDはともに4cmと1cmを他の二辺とする直角三角形の斜辺ですから、三平方の定理よりBD=GD=√17cmであると分かります。

BGはBC=CD=1cmの直角二等辺三角形の斜辺ですから、√2cmと分かります。

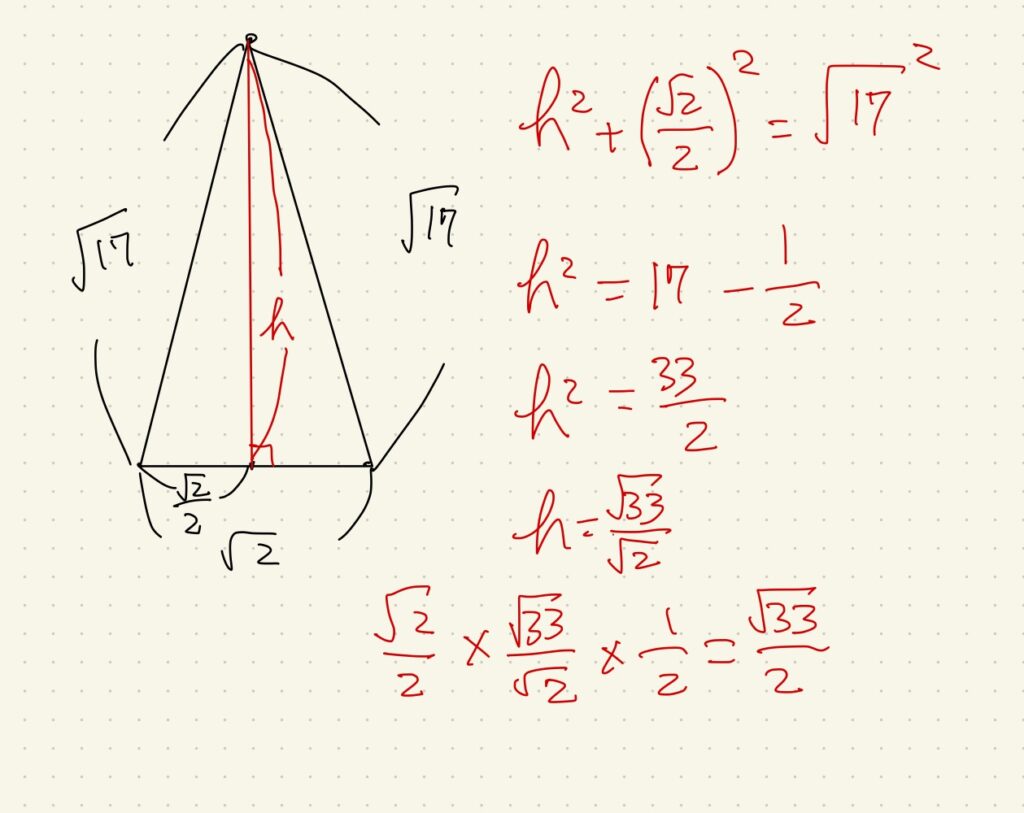
この二等辺三角形はさっと頂角から垂線を引けば合同な直角三角形が2枚出ます。

二等辺三角形と正三角形はこれで三平方の定理を使えば高さが出ます。

非常に典型的な問題ですので、作図さえしておけば赤ペンの式が書けたはずです。

ここまでは絶対に押さえましょう。

(ウ)最後の立体の最短距離問題も非常に典型的でした。

展開図を描こうというごくごく当たり前の手順を踏めば勝てます。

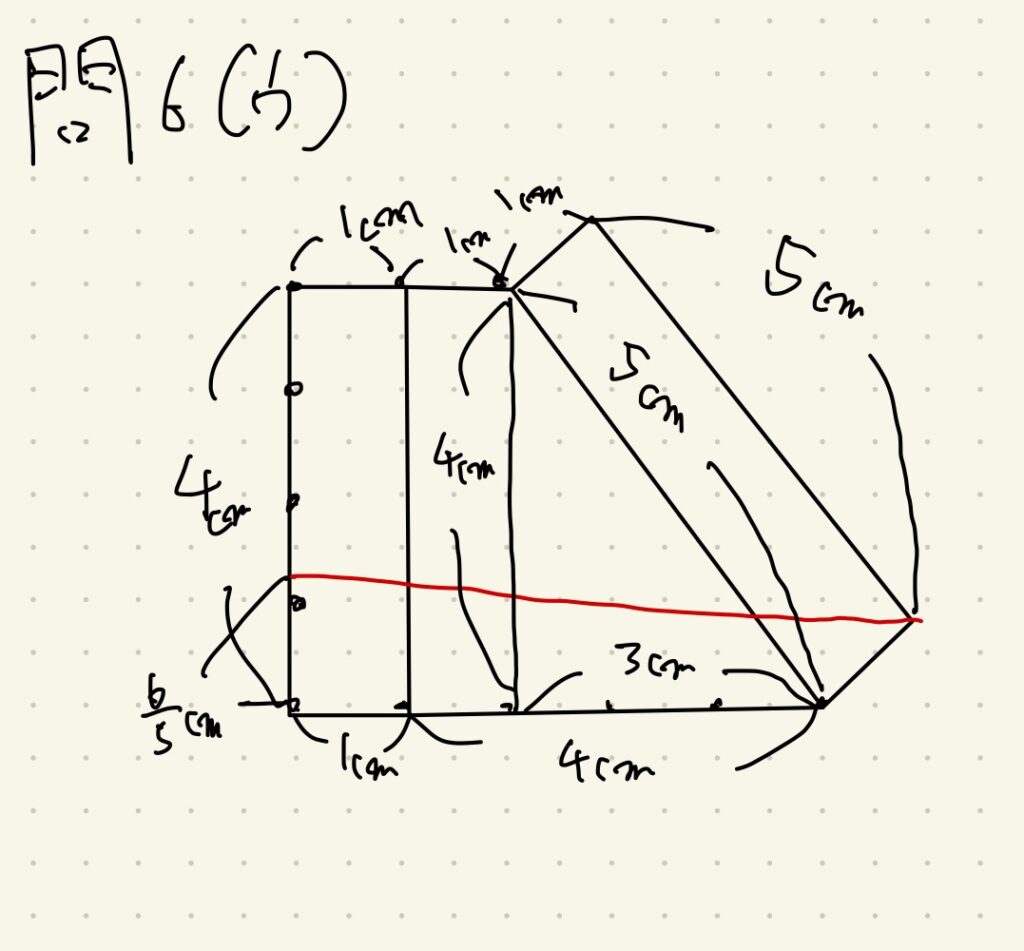
赤線部分が求める長さになります。

しかしこれだけでは都合のいい図形の一部として赤線を扱えませんので、どうにもなりません。

斜めの長さは三平方の定理を使うという定石を考えれば直角三角形が欲しいところです。

できればすでに分かっている「3:4:5」を使えるものがありがたいです。

そこで、上の図形の右下に直角をとってみると、相似な青い三角形が見えてきました。

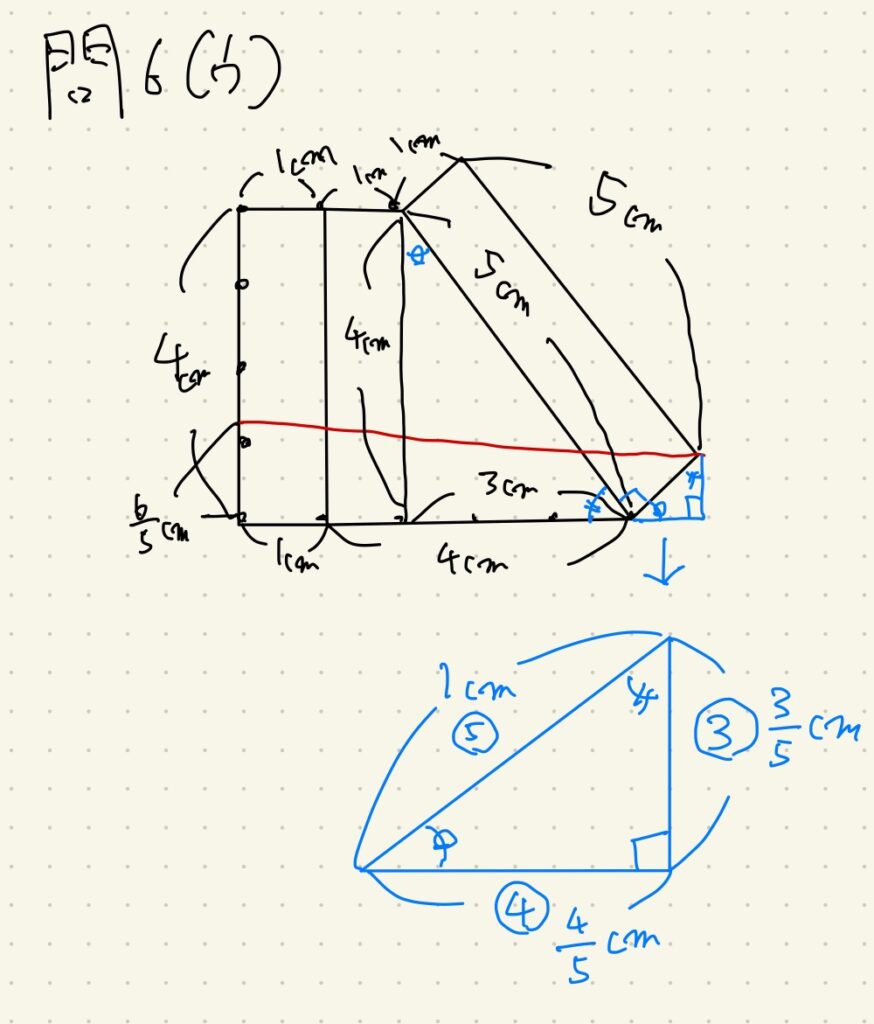
一直線に直角が接している場合には、直角以外の部分の角の和が90°になります。

これを使えば直角三角形を増やせるというわけです。

幸い斜辺の1cmが分かっていますから、残り二辺は即分かります。

この数値を使えば以下のような作図が可能です。

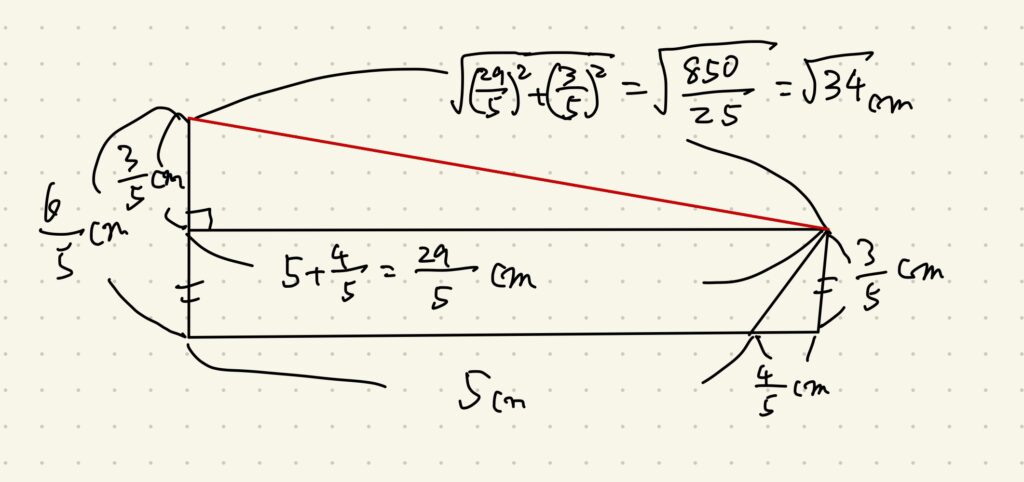
これで赤線を斜辺とする直角三角形の二辺が求められました。

後は三平方の定理で終了です。

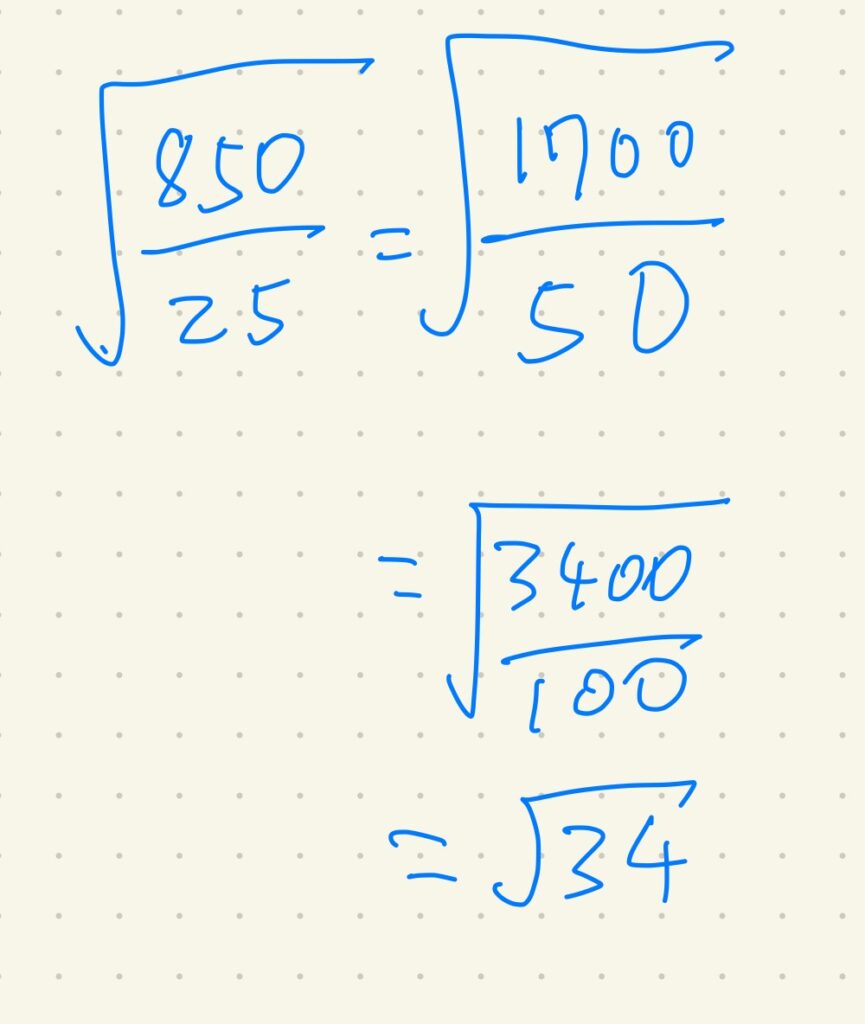
ちなみに平方根の中身を普通に割り算しても良いですが、上のように分母を100にしてしまえば、割り算を回避できるという考えもあります。

今回はそこまで有効とは言えませんが、小技としては持っておきたいです。

問6の講評としては、使う技術は高度ではないが作図や計算速度などが要求される点、そのための時間を残しておけたかという戦術が問われる一問でした。

全体講評

恐らく数学だけ見れば、平均点は下がるはずです。

他教科とのバランスにもよりますが、これは教科書改訂後の参考となる問題だったと言えます。

前回の2021年の問題が範囲の上で参考にしにくかったことを考えても、この計算量を標準とするでしょう。

来年度以降の受験生諸君には、徹底的に基本となる解法と対応速度を磨いてもらいたいところです。