相似な図形の探し方 平行四辺形編
今日は中3の生徒と図形の問題について話をしていました。
日頃テンポよく演習を進めるこの生徒が珍しく回答速度が遅かったのが図形、とりわけ相似を使った問題でした。
生徒曰く「相似を使って解くのはわかるのだが、探すのに手間取っている」ということでした。
一旦相似を発見すれば、後の計算量は大したことがありませんからね。
神奈川県の県立高校入試問題で言えば2020年大問3(ウ)あたりが対象になるものでしょう。
平行四辺形に線分が引かれているタイプが典型です。
これらの問題は平行線がヒントになります。
平行線があるということは錯角がとりやすいということですから、意識すれば相似がとりやすいです。
また、そもそも相似を探す際に「どの辺とどの辺の比が知りたいのか」を強く意識します。
比べたい二組の辺を相似の対応する比とできる三角形を探すために平行線を使います。
もし片方の辺に対応する三角形が見つけられなかったらどうするかも考えます。
というより、入試レベルで言えば片方は三角形が明示されていないことが大半です。
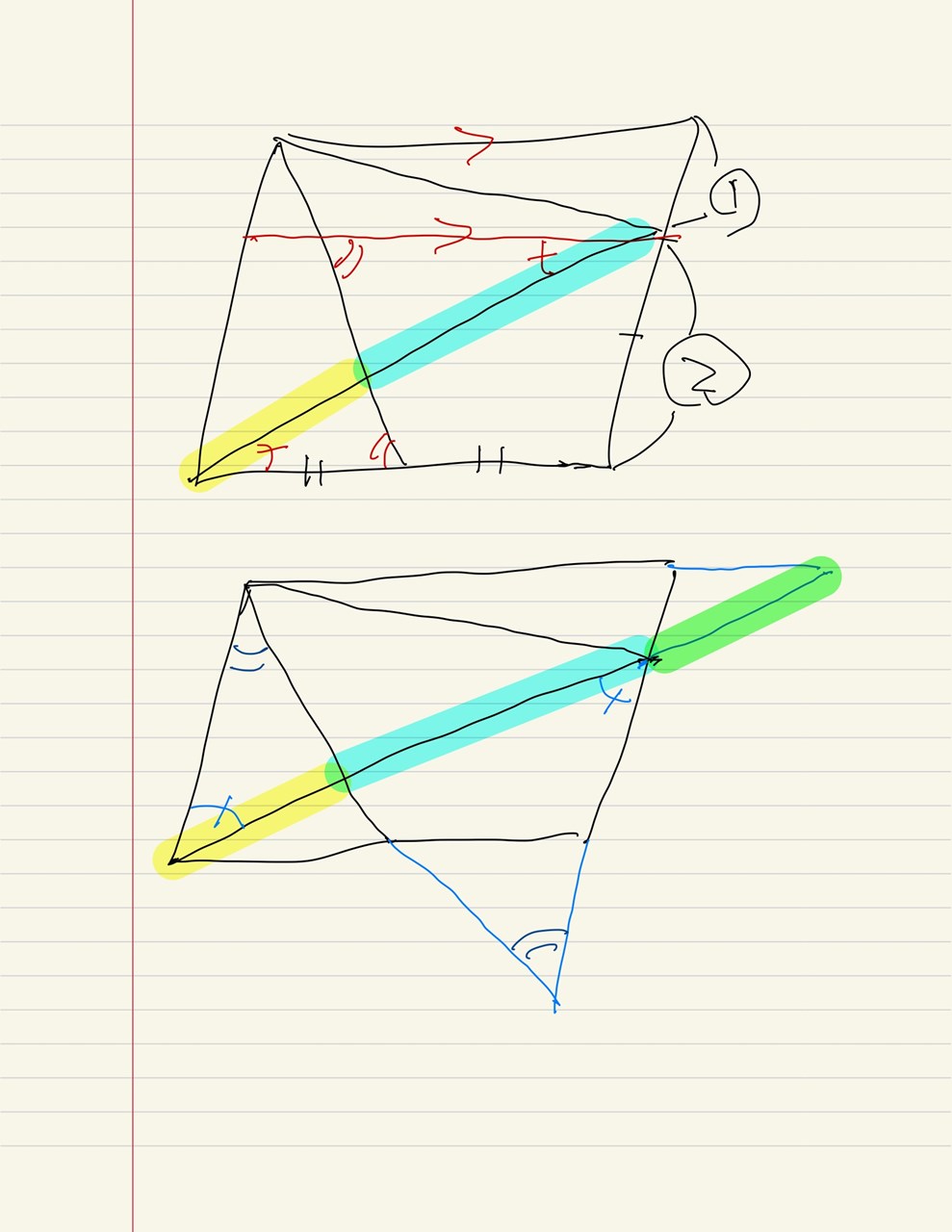
その場合には元の平行四辺形の辺と平行に別の補助線を引くことで解決できる場合があります。
平行四辺形の内部に引くイメージでいきましょう。
あるいは、平行四辺形の辺以外の線分を延長して四角形を三角形にしてしまうことで相似を作り出すことも有効です。
前者が下の画像の赤パターンの補助線、後者が青パターンの補助線です。
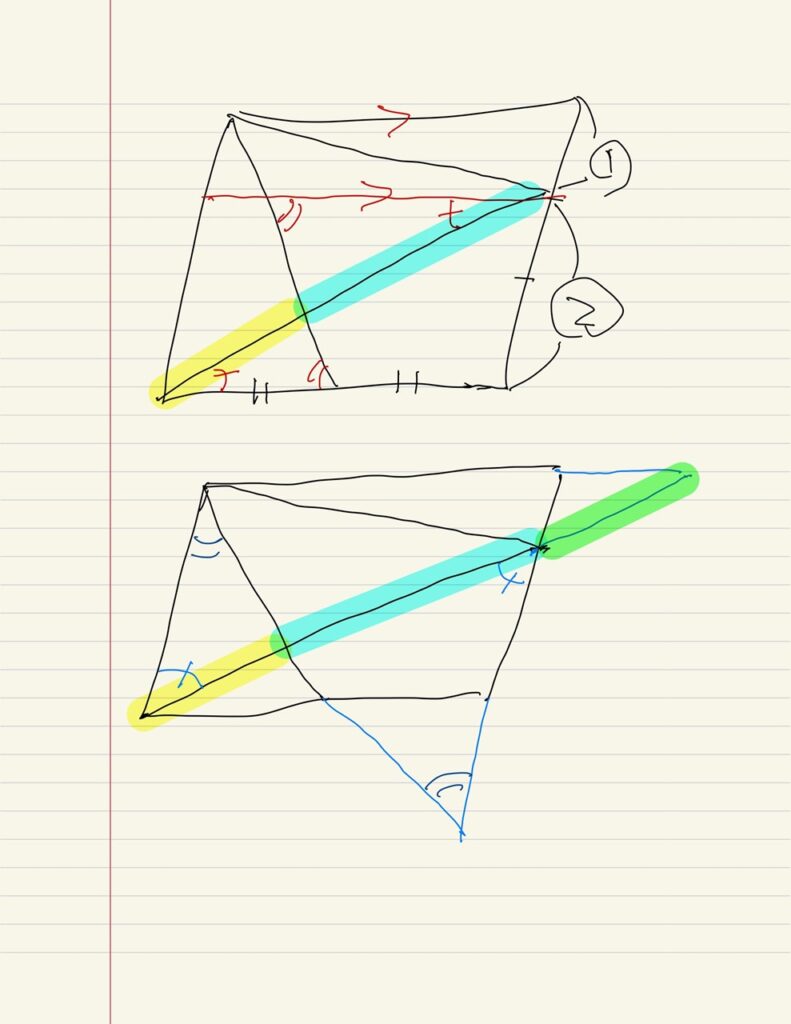
青パターンのように引く際には「伸ばした二本の線分が交わるように」と考えておけば迷いにくいです。
どのような問題であっても攻略法は必ずルールに出来ます。










