汎用性の高い学習

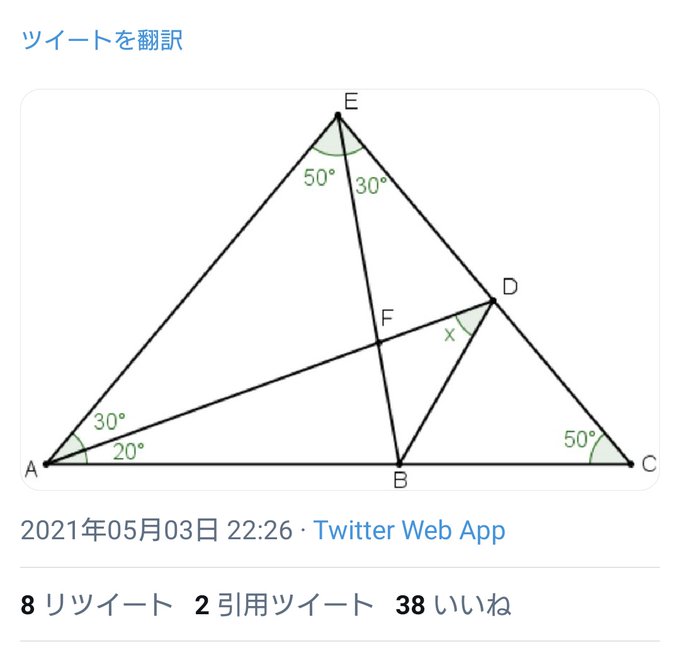
受験生と立体図形の問題について考えていました。

受験生がある視点で問題を解釈して、正解となる数値を出してくれました。

ただ、その答案の過程で感覚に頼った推論をし、その推論が正しいことの証明が出来ない答案でした。

塾長からはその推論がどのようにすれば正しいと証明できるかについて話をしました。

その上で別解となる答案の構成について説明をしました。

生徒の答案の方が計算量は少なく済むものでしたが、あえて別解での答案も自分で書いてみるように指示をしました。

基本的に計算量の多い答案は避けたほうが無難です。

計算をするということはその分だけ計算ミスが発生する可能性も上がりますし、遅くなります。

ではなぜ今回は別解答案も練習してもらったのかといいますと、汎用性の問題です。

生徒の答案は一つ条件を変えるだけで途端に使えなくなる特殊な解法でした。

特殊な解法でも増やしておくことは実力につながります。

しかし、それは基礎基本となる汎用性の高い解法をマスターした後に来る段階です。

定期テストで点数を上げるというだけなら特定の先生の過去問を対策しておくのが楽です。

そうやって点数を上げても県立高校入試や大学入試で同じ作戦が使えるかと言えば、そうではないです。

この場合の特定の先生の過去問が特殊な解法に当たるもので、汎用性が低い学習と言えるのと同じです。

あくまで入学試験本番やその先の学習の土台となってくれる基礎基本を徹底していくことが、優先です。

遠回りにみえてもまずやるべきことから積み重ねていきましょう。