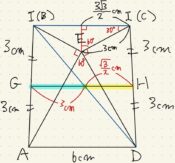
平行四辺形中の線分比問題は相似で解決

今日はテストゼミの解説授業日でした。

最後のいわゆる「合否判定の参考」となるデータを配布しました。

あくまで過年度の先輩方と比較してのデータですから参考程度ではありますが、それでも自分のやってきたことを確かめる最後の確認ということです。

青木学院の受験生は3社の模擬試験を受けてもらっています。

異なる部分を含む母集団でのデータチェックと、異なる傾向の問題に触れてもらうことでの弱点徹底攻略のためです。

同じ傾向のものだけに慣れてしまうと、いざ出題形式や傾向が変わったときに対応できません。

試験本場で力を発揮するためには「動じない自分」を様々な面から作り上げていくことも必要です。

そのために必要なことが出題パターンへの対応力であり、そもそもの骨太な学力です。

結局私たちが問われていることは・試されていることは・求められていることは何かを把握すると、自分が答案を作る土台が揺るぎません。

その土台にのせていくものに多少の差異はあれども、やるべきことはシンプルなのです。

例えば平行四辺形を分割した線分比という受験の定番問題があります。

「線分比を求めるには相似比がもっともシンプルである」

「相似比を求めるには三角形の相似が役立つ」

「相似な三角形は平行線で作るのが分かりやすい」

「平行線が足りなければ引いてしまえばいい」

これらの考えがあれば、どんな問題でもなんとかなります。

自分が問題を解くときに、上記のどこで躓いているのかをきちんと見極めてください。

その上で比の問題を解くときに、最初はこれらの考え方を軽くメモしたり思い出したりしてから解いてみるとよいです。

慣れると無意識に解けるようになります。

その日まではコツコツと地味な努力をしましょうね。