「確実に正しいと言える」ことが数学のルール
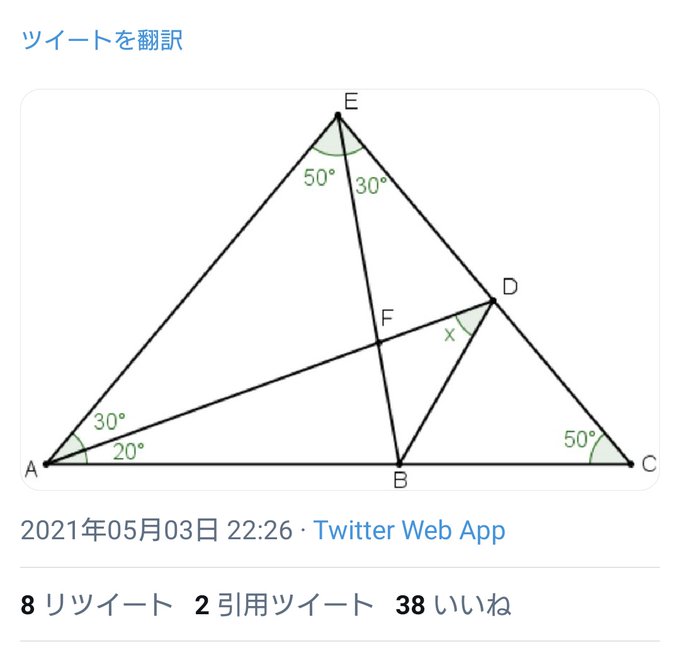
数学の答案はいくつかの道で正解に辿り着けます。
しかしそのどれもが、「確実に正しいと言える」ことで構成されてます。
知識を理屈で積み重ねたもののみが数学の答案だと言えます。
数学が苦手な生徒は普段から理屈で物事を考え慣れていません。
「何故そうしていいのか?」が極端に弱く、「そう思ったから」程度のことしかありません。
「何故その式を書いたの?」「こう思ったから」
「何故その数字だと思ったの?」「そう思ったから」
「どうしてこの行を書いたの?」「そう見えたから」
万事この調子で生きてきたのでしょう。
考えずに生きてきた結果、数学が苦手になっているわけです。
考えること、考えを言語化して整理すること、伝えることを求められなかった人生なのでしょう。
これは、いくらかは親の責任です。
子供に何かを伝えるときに、理屈で伝えてないのではないでしょうか?
子供の考えを、言葉で掘り下げる対話をしてこなかったのではないでしょうか?
それなのに子供に理屈で考えて言葉で表現することを求めても、慣れていない子供が出来るわけがないです。
その人生を10年積み重ねた時点で、もう大分ハンデになっているのです。
ですから、青木学院では徹底して理屈を使ってもらいます。
伝える側も理屈をこめて伝えます。
理屈に乗せて表現することを求めます。
個別演習と言う形式は演習が基本にあります。
それは演習を通じて学力を鍛えることであり、演習後の塾長との対話を通じて理屈に慣れてもらうことでもあります。
徹底てして能動的に脳をつかってもらうのです。
それなりに時間はかかりますが、必ず結果に結びつきます。