繰り返さずに身に着けるほど器用なのか？

難しく思えることに対しては様々なアプローチがあります。

今日は中3に図形の内角の和についての問題を出して「ヒマなときや気分転換に解きな」と伝えました。

しばらくして解いてきた生徒に手順を説明してもらい、ふんふんと塾長は聞いていました。

外角をうまく利用して立式していく解法でした。

「別解はありますか？」と中3に尋ねられたので「分からん！でもあるやろ」と塾長は返します。

実のところ問題を見かけて生徒に出そうとメモしておいただけなので、解かずに生徒にみせたんです。

ですから、初見に近い問題だったので解法は全く頭になかったんです。

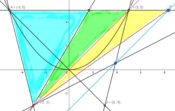
ペンとペーパーを出して作図し、ボールペンでサクサクと記号や補助線を書き込んで別解を2つ示しました。

四角形の3つ内角の和の移動を利用する解法と、内閣を分割して三角形と星型を作って解く解法です。

「よく分からんけど、あと1つか2つは別解が作れるやろうね」と伝えます。

こういうことをやると、「どうして塾長はそんな風に解けるんですか？」と聞かれます。

いくつか理由はありますが、たぶん二番目に真似しやすい作戦は「ひたすら解きまくった」という反復でしょう。

特段何かの才能に恵まれたわけでもないけど何かを習得したいと考えるなら、きちんとした理屈を学んだうえで反復することです。

ピアノを弾ける人ってすごいじゃないですか。

左右の手が違う動きが出来る上に、一定の定められたものとして他人と共感できるわけですから。

あれだって滅茶苦茶反復して練習してるでしょう。

それと同じように、図形の問題を解きまくってその中から作戦を見出して身に着けていくのが一番です。

手間がかかりますが、間違いなく最強です。

因みに一番目に真似しやすい作戦は、日ごろの塾長が問題をどのように解いているかを見てるとすぐに分かるんです。

知りたい人は、塾長に図形の質問に来て下さい。