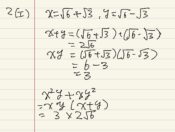x^3-y^3-z^3-3xyz 因数分解

$$x^3-y^3-z^3-3xyz$$
の因数分解を考えます。
暗記している公式から因数分解する
$$(x-y)^3=x^3-3x^2y+3xy^2-y^3$$
この公式は暗記している人が非常に多いので、ここから式を動かしてみます。
$$(x-y)^3+3x^2y-3xy^2=x^3-y^3$$
これを使って、三乗の部分を上手く処理してみます。
$$x^3-y^3-z^3-3xyz$$
$$=(x^3-y^3)-z^3-3xyz$$
$$=\color{red}{(x-y)^3+3x^2y-3xy^2}-z^3-3xyz$$
$$=\color{red}{(x-y)^3-z^3}+3x^2y-3xy^2-3xyz$$
ここで、$(x-y)^3=A^3$と見ると、また三乗の処理が可能です。
$$=\color{red}{(x-y-z)^3+3(x-y)^2z-3(x-y)z^2}+3x^2y-3xy^2-3xyz$$
$$=(x-y-z)^3+3(x-y)^2z-3(x-y)z^2+3x^2y-3xy^2-3xyz$$
$$=(x-y-z)^3+3(x-y)^2z-3(x-y)z^2+color{red}{3xy(x-y-z)}$$
$$=(x-y-z)^3\color{red}{+3(x-y)z\{(x-y)-z\}}+3xy(x-y-z)$$
$$=(x-y-z)^3\color{red}{+3(x-y)z(x-y-z)}+3xy(x-y-z)$$
$$=(x-y-z)\color{red}{\{(x-y-z)^2+3(x-y)z+3xy\}}$$
$$=(x-y-z)\color{red}{(x^2+y^2+z^2-2xy+2yz-2zx+3zx-3yz+3xy)}$$
$$=(x-y-z)(x^2+y^2+z^2\color{red}{+xy-yz+zx)}$$
注目しやすい部分から合成する
式の中に$x^3-y^3-z^3$があるので、
$$(x-y-z)(x^2+y^2+z^2)=\color{red}{x^3-y^3-z^3}+xy^2+xz^2-yx^2-yz^2-zx^2-^zy^2$$
を手がかりとしてみます。
上の式から
$$(x-y-z)(x^2+y^2+z^2)\color{red}{-xy^2-xz^2+yx^2+yz^2+zx^2+zy^2}=x^3-y^3-z^3$$
$$(x-y-z)(x^2+y^2+z^2)-xy^2-xz^2+yx^2+yz^2+zx^2+zy^2\color{red}{-3xyz}=x^3-y^3-z^3\color{red}{-3xyz}$$
として、右辺を問題の形に合わせます。
左辺でなんとかしたいのが$-xy^2-xz^2+yx^2+yz^2+zx^2+^zy^2-3xyz$です。
左辺の$(x-y-z)$でくくれたら嬉しいので、以下のように変形します。
$$-xy^2-xz^2+yx^2+yz^2+zx^2+^zy^2-3xyz$$
$$=(yx^2-xy^2-xyz)+(-xyz+zy^2+yz^2)+(zx^2-xyz-xz^2)$$
$$=xy(x-y-z)-yz(x-y-z)+zx(x-y-z)$$
$$=(x-y-z)(xy-yz+zx)$$
これを元の式にあてはめると
$$(x-y-z)(x^2+y^2+z^2)+\color{red}{(x-y-z)(xy-yz+zx)}=x^3-y^3-z^3-3xyz$$
$$(x-y-z)(x^2+y^2+z^2+xy-yz+zx)=x^3-y^3-z^3-3xyz$$
となって、因数分解ができます。
また、以下を公式とする参考書も多いです。
$$x^3+y^3+z^3-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)$$
これに元の式の文字を当てはめても因数分解できます。